— 1. Introdução —
Não existe uma função sem domínio, sem contradomínio e sem imagem. Os três elementos citados são inseparáveis a função.
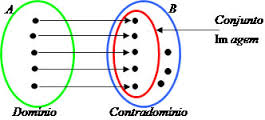
Sendo assim, vamos, então começar a definir os três elementos fundamentais da função. Seja a função :
. Por diagrama, temos:

| Definição 1 -Chama-se domínio da função |
| Definição 2 – Chama-se contradomínio da função |
— 2. Determinação do domínio, do contradomínio e da imagem da função —
| Exercício 1 Determinar o domínio, o contradomínio e a imagem da função.
Resolução
-O domínio é
-O contradomínio é
-A Imagem é |
Obs:O leitor terá que ler a matéria de conceito de função disponível nesse mesmo blog.
| Exercício 5
Dada a função Determinar:
Resolução
|
| Exercício 6
Na função real Resolução
Como a função é real então
|
— 3. Determinação da imagem da função quadrática —
Dada a função geral,
se a imagem será
se a imagem será
| Exercício 8
Determinar a imagem da função Resolução
Primeiro, vamos determinar os coeficientes
segundo, vamos determinar o
Por fim, temos:
Como
|
| Exercício 9
Determinar a imagem da função Resolução
Primeiro, vamos determinar os coeficientes
Segundo, vamos determinar o
Por fim, temos:
Como |






otimos exercicios
GostarGostar
A resolução do exercício 5 usa a função apresentada no exercício 7, e a resolução do exercício 7 vice versa…
GostarLiked by 1 person
{ d)} Como { \dfrac{3}{3}\notin\mathbb{Z} },temos: { f(\dfrac{3}{2})=(\dfrac{3}{2})^2 \leftrightarrow f(\dfrac{3}{2})=\dfrac{9}{4} }.
ainda outro erro, 3/3 = 1, como tal se fosse este o valor apresentado na alinea d) o mesmo pertence ao grupo dos Z…
GostarGostar
Muito ruim a resolução no exercício 4,foi direto sem explicação,
em f(-6)= -6 +2. que dois é esse?
GostarGostar
o exercício 9 está errado -4x-3x-3 é -36
6 ao quadrado é 36 -36 =0 e não 72
GostarGostar
Esta corecta a resoluçao tenx k prestar os sinais
-4×(-3)×3=+36
GostarGostar
Copiaram erradamente a funçao na resoluçao. seria -3x²+6x+3, e nao -3x²+6x-3
GostarGostar
OLÁ,Gostei das resoluções desse site, mais fiquei em duvidas na resolução da questão três, como eu já sei minha imagem, sem fazer o calculo, na hora da ligações do elementos, fiquei perdida. Alguém pode me ajudar?
GostarGostar
Essa figura apenas é um exemplo de funçao. Nao se calcula nada. O importante era pra demonstrar o domínio ou conjunto d Objectos, q sao os elementos d A ou ond partem as setas. E o contradominio ou imagem sao os elementos de B mas q tem pelomenos um correspondent em A. Espero ter t ajudad
GostarGostar
Oy gostei muito da resoluçao dos problemas, sugiro k nas proximas ocasioes incluem problemas como funçoes compostas e radiciaçao…
GostarGostar
TUDO ERRADO,TUDO ERRADO.
GostarGostar