Início » 2016 » Fevereiro

Monthly Archives: Fevereiro 2016

Aplicação das equações diferenciais de primeira ordem.Misturas

02/28/2016 1:43 pm / Deixe um comentário

— 3.5. Misturas —

Fazer uma mistura é um procedimento extremamente rotineiro em nossas vidas. Com certeza, todos nós já fizemos uma ou várias. Uma mistura é constituída por duas ou mais substâncias, sejam elas simples ou compostas. As proporções entre os constituintes de uma mistura podem ser alterados por processos químicos, como a destilação. Todas as substâncias que compartilham um mesmo sistema, portanto, constituem uma mistura. Não se pode, entretanto, confundir misturar com dissolver. Água e óleo, por exemplo, misturam-se mas não se dissolvem. Isso torna o sistema água ${+}$ óleo uma mistura, não uma solução.

Figura 1:Mistura da água e o óleo

A mistura de dois fluidos algumas vezes dá origem a uma equação diferencial de primeira ordem.Nos problemas de misturas se deseja calcular a quantidade de uma substancia ${Q(t)}$ que há em um recipiente em qualquer instante ${t}$ .

Vamos supor que um tanque contenha uma mistura de água e sal com um volume inicial de ${V_{0}}$ litros e ${Q_{0}}$ gramas de sal e que uma solução salina seja bombeada para dentro do tanque a uma taxa de ${q_{e}}$ litros por minuto possuindo uma concentração de ${C_{e}}$ gramas de sal por litro.Suponha que a solução bem misturada sai a uma taxa de ${q_{s}}$ litros por minuto.

A taxa de variação da quantidade de sal no tanque é igual a taxa com que entra sal no tanque menos a taxa com que sai sal no tanque.

$\displaystyle \dfrac{dQ}{dt}={Taxa \quad de \quad entrada \choose de \quad sal}-{Taxa \quad de \quad saida \choose de \quad sal}$

$\displaystyle \dfrac{dQ}{dt}=R_{e}-R_{s} \ \ \ \ \ (1)$

A taxa com que entra sal no tanque é igual a taxa com que entra a mistura, ${q_{e}}$ , vezes a concentração de entrada, ${C_{e}}$ , ou seja:

$\displaystyle R_{e}=q_{e}\cdot C_{e} \ \ \ \ \ (2)$

E a taxa com que sai sal do tanque é igual a taxa com que sai a mistura do tanque, ${q_{s}}$ , vezes a concentração de sal que sai do tanque, ${C_{s}}$ ,ou seja:

$\displaystyle R_{s}=q_{s}\cdot C_{s} \ \ \ \ \ (3)$

Como a solução é bem misturada a concentração de sal que sai do tanque, ${C_{s}}$ , é igual a concentração de sal no tanque, isto é:

$\displaystyle C_{s}=\dfrac{Q}{V} \ \ \ \ \ (4)$

onde ${V}$ é o volume no tanque.

Como o volume no tanque, ${V}$ , é igual ao volume inicial, ${V_{0}}$ , somado ao volume que entra no tanque menos o volume que sai do tanque, então:

$\displaystyle V=V_{0}+(\vartriangle q)t \ \ \ \ \ (5)$

onde ${\vartriangle q=q_{e}-q_{s}}$

Assim, a quantidade de sal no tanque, ${Q}$ , é a solução do problema de valor inicial

$\displaystyle \left\{\begin{array}{ll} \dfrac{dQ}{dt}=q_{e}C_{e}-q_{s}\dfrac{Q}{V_{0}+(\vartriangle q)t}\\ Q(0)=Q_{0} \end{array}\right. \ \ \ \ \ (6)$

Distingue-se os seguintes casos particulares:

${q_{e}=q_{s}}$ . O volume é constante
${q_{e}>q_{s}}$ . O volume aumenta
${q_{e}<q_{s}}$ . O volume diminui

Figura 2:Tanque com uma mistura

Exemplo 1 Em certo tanque ha ${180}$ litros de solução salina que contem 10Kg de sal.Despeja-se água no tanque com uma velocidade de ${4}$ litros por minuto e sai a mistura com velocidade de ${3}$ litros por minuto .A concentração se mantém homogénea.Achar a quantidade de sal depois de meia hora.

Solução:O exemplo nos fornece os seguintes dados

Volume inicial: ${V_{0}=180l}$
Quantidade de sal: ${Q_{0}=10Kg}$
Velocidade da agua ao entrar: ${q_{e}=4l/min}$
Velocidade da agua ao sair: ${q_{s}=3l/min}$
concentração de sal no inicio: ${C_{e}=0}$ .A água entra sem sal

Se ${Q}$ é a quantidade de sal no tanque em um dado momento.O volume de solução salina em qualquer momento é

$\displaystyle V=V_{0}+(q_{e}-q_{s})t$

a concentração de sal é:

$\displaystyle C=\dfrac{Q}{V}=\dfrac{Q}{V_{0}+(q_{e}-q_{s})t}$

a quantidade de sal no tanque, ${Q(t)}$ , é a solução do problema de valor inicial

$\displaystyle \left\{\begin{array}{ll} \dfrac{dQ}{dt}=-q_{s}\dfrac{Q}{V_{0}+(q_{e}-q_{s})t}\\ Q(0)=Q_{0} \end{array}\right. \ \ \ \ \ (7)$

$\displaystyle \left\{\begin{array}{ll} \dfrac{dQ}{dt}=-3\dfrac{Q}{180+(4-3)t}\\ Q(0)=10 \end{array}\right. \ \ \ \ \ (8)$

A equação ${(8) }$ é linear e pode ser escrita como

$\displaystyle \dfrac{dQ}{dt}+3\dfrac{Q}{180+t}=0 \ \ \ \ \ (9)$

Um fator integrante é neste caso

$\displaystyle \mu (t)=e^{\int \frac{3}{180+t}}dt=e^{3\ln(180+t)}=(180+t)^{3}$

multiplicando a equação ${(9)}$ por ${\mu (t)}$ obtemos:

$\displaystyle (180+t)^{3}\dfrac{dQ}{dt}+3Q(180+t)^{2}=0 \Rightarrow \dfrac{d}{dt}\left[(180+t)^{3}Q\right]=0$

Integrando-se obtemos:

$\displaystyle (180+t)^{3}Q=c$

ou seja,

$\displaystyle Q=\dfrac{c}{(180+t)^{3}}$

substituindo ${t=0}$ e ${Q=10 \Rightarrow c=58\cdot32\times 10^{6}}$

substituindo o valor de ${c}$ encontrado temos:

$\displaystyle Q=\dfrac{58\cdot32\times 10^{6}}{(180+t)^{3}}$

para ${t=30}$ , a quantidade de sal depois de meia hora será:

$\displaystyle Q(30)=6.3 kg$

Exemplo 2 Um tanque com a capacidade de ${400}$ litros contem inicialmente ${200}$ litros de uma mistura de sal e agua (salmoura) com ${30}$ gramas de sal dissolvidos.Despeja-se uma solução com ${1}$ grama de sal por litro a uma taxa de ${4}$ litros por minuto; a mistura se mantém uniforme mediante a agitação e do sal a uma taxa de ${2}$ litros por minuto.Calcule a quantidade de gramas de sal no tanque no momento em que começa a transbordar.

Solução: o exemplo nos fornece os seguintes dados:

Volume no tanque: ${V=400l}$
Volume inicial: ${V_{0}=200l}$
Quantidade de sal dissolvido: ${Q_{0}=30gr}$
Concentração de sal que entra: ${C_{e}=1gr/l}$
Velocidade da solução ao entrar:; ${q_{e}=4l/min}$
Velocidade da mistura ao sair: ${q_{s}=2l/min;}$

o objetivo é achar ${Q(t_{f})}$ onde ${t_{f}}$ é o tempo que o tanque leva para encher.Mas primeiro vamos achar a quantidade de sal (em gramas) ${Q(t)}$ no tanque em qualquer instante ${t}$ antes de transbordar.A taxa de variação ${Q(t)}$ é:

$\displaystyle \dfrac{dQ}{dt}=R_{e}-R_{s} \ \ \ \ \ (10)$

A taxa de entrada ${R_{e}}$ de sal é:

$\displaystyle R_{e}=q_{e}C_{e}=4\cdot 1=4gr/min$

A taxa de saída ${R_{s}}$ de sal é:

$\displaystyle R_{s}=q_{s}C_{s}=2.\dfrac{Q}{V}$

onde ${V}$ é volume do tanque no instante ${t}$ .Como no tanque entra ${4l/min}$ e sai ${2l/min}$ o liquido acumulara no tanque uma taxa de:

$\displaystyle \vartriangle q=q_{e}-q_{s}=4-2=2l/min$

Naturalmente, o tempo que demora a encher o tanque é

$\displaystyle t_{f}=\dfrac{\vartriangle V}{\vartriangle q}=\dfrac{200}{2}=100min$

mas,

$\displaystyle V(t)=V_{0}+(\vartriangle q)t=200+2t=2(100+t)$

substituindo ${V(t)}$ na equação da taxa de saída do sal teremos:

$\displaystyle R_{s}=q_{s}C_{s}=2.\dfrac{Q}{2(100+t)}=\dfrac{Q}{(100+t)}$

ao substituir ${R_{e}}$ e ${R_{s}}$ na equação ${(10)}$ obtemos o seguinte problema de valor inicial

$\displaystyle \dfrac{dQ}{dt}=4-\dfrac{Q}{t+100}; \quad Q(0)=30 \ \ \ \ \ (11)$

a equação ${(11)}$ é uma equação diferencial linear, e pode ser escrita da seguinte forma:

$\displaystyle \dfrac{dQ}{dt}+\dfrac{Q}{t+100}=4$

o fator integrante neste caso será:

$\displaystyle \mu (x)=e^{\int \frac{dt}{t+100}}=e^{\ln (t+100)}\Rightarrow \mu (x)=(t+100)$

multiplicando a equação ${(11)}$ por ${\mu (x)}$ , teremos:

$\displaystyle (t+100)\dfrac{dQ}{dt}+(t+100)=4(t+100)\Rightarrow \dfrac{d}{dt}\left[Q(t+100)\right]=4(t+100)$

Integrando-se obtemos:

$\displaystyle Q(t)=2(t+100)+\dfrac{C}{t+100}$

Aplicando a condição inicial ${Q(0)=30}$ obtemos: ${C=-17000}$ . por tanto a solução ao PVI é:

$\displaystyle Q(t)=2(t+100)-\dfrac{17000}{t+100}$

Para ${t_{f}=100, }$ a quantidade de sal no momento que transborda é

$\displaystyle Q(100)=315gramas$

Porquê o peixe parece maior? Refração em superfície esférica.

02/27/2016 12:47 am / Deixe um comentário

— 2.7.16. Refração em superfície esférica —

Já analisamos a refração sobre um dióptro plano, onde vimos que, dependendo da relação entre os índices de refração, poderemos ver a imagem mais longe ou mais perto do que ela realmente está. Mas, o dióptro plano não produz a sensação de que o objecto é transversalmente maior ou menor, ou seja, quando a superfície de separação é plana, não temos ampliação transversal. Um exemplo disto é observarmos um peixe num lago, ou observarmos um peixe a partir da face plana de um aquário de faces planas.

Já, se observamos a imagem de um peixe que está num aquário esférico, em certas posições, notamos uma ampliação transversal da imagem, ou seja, o peixe parece maior do que ele realmente é. As razões desta aparente ampliação são explicadas pela refração em superfícies esféricas.

Figura 58: Refração em superfície esférica. [5] Adaptado

Consideremos a situação da figura 58, onde os raios incidentes que convergem no ponto ${P}$ , refratam-se pela superfície esférica, convergindo no ponto ${P'}$ . Neste caso, ${P}$ é o objecto real e ${P'}$ é a imagem real. A superfície esférica tem centro em ${C}$ e raio ${R}$ . Os índices de refração dos dois meios são ${n_a}$ e ${n_b}$ com ${n_a<n_b}$ . Um raio que incide no ponto ${P}$ pela direcção normal à superfície, ao refratar-se não sofre nenhum desvio, e passa pelo centro ${C}$ (de acordo com a lei de Snell-Descartes) e pelo ponto ${P'}$ (que é imagem de ${P}$ ). Um raio vindo do ponto ${P}$ que incida num ponto ${B}$ da superficial, ao refrata-se, vai necessariamente passar pelo ponto ${P'}$ , visto que este é imagem de ${P}$ . A recta que passa sobre o segmente ${BC}$ é a normal à superfície no ponto ${B}$ . Logo, podemos definir ${\theta_a}$ como ângulo de incidência em ${B}$ e ${\theta_b}$ como ângulo de refração. Então:

$\displaystyle n_a \cdot \sin\theta_a = n_b \cdot \sin \theta_b \ \ \ \ \ (51)$

Sendo ${d}$ a distância do objecto e ${d'}$ a distância da imagem, e dado ${\delta=VQ}$ , nos triângulos rectângulos ${PBQ}$ , ${CBQ}$ e ${P'BQ}$ podemos obter:

$\displaystyle \tan \alpha=\frac{h}{ d +\delta } \qquad \tan \beta=\frac{h}{ d' - \delta } \qquad \tan \phi=\frac{h}{ R- \delta } \ \ \ \ \ (52)$

Note que ${VC=R}$ .

Para raios paraxiais, todos os ângulos serão muito pequenos, então, será válida a aproximação ${\tan \alpha \approx \sin\alpha\approx \alpha}$ . Logo, as equações 51 e 52 ficam:

$\displaystyle n_a \cdot \theta_a = n_b \cdot \theta_b \ \ \ \ \ (53)$

$\displaystyle \alpha=\frac{h}{ d +\delta } \qquad \beta=\frac{h}{ d' - \delta } \qquad \phi=\frac{h}{ R- \delta } \ \ \ \ \ (54)$

Analisando o triângulo rectângulo ${PBC}$ , considerando que o ângulo interno sobre o vértice ${B}$ deve ser ${180^0-\alpha-\phi}$ (do teorema de ângulos internos de um triângulo) e também deve ser igual á ${180^0-\theta_a}$ (por ser suplementar deste); e analisando o triângulo ${P'BC}$ onde, no vértice ${C}$ , o ângulo interno deve ser ${180^0-\theta_b - \beta}$ e também deve ser ${180^0-\phi}$ , obtemos então:

$\displaystyle \theta_a=\alpha+\phi \qquad \phi =\theta_b + \beta \Rightarrow \theta_b =\phi - \beta \ \ \ \ \ (55)$

Substituindo os valores de ${\theta_a}$ e ${\theta_b}$ da equação 55 na equação 53, obtemos ${ n_a\cdot(\alpha+\phi)=n_b\cdot(\phi - \beta)}$ . Organizando a expressão, obtemos:

$\displaystyle n_a\cdot\alpha+n_b \cdot \beta =(n_b-n_a)\cdot\phi \ \ \ \ \ (56)$

Substituindo ${\alpha}$ , ${\beta}$ e ${\phi}$ pelos valores da equação 54 na equação 56 e simplificando ${h}$ , obtemos:

$\displaystyle \frac{n_a}{ d +\delta } + \frac{n_b}{ d' - \delta } =\frac{n_b-n_a}{ R- \delta } \ \ \ \ \ (57)$

Lembrando que para raios paraxiais, ${\delta}$ tende para zero, logo, obtemos:

$\displaystyle \frac{n_a}{ d } + \frac{n_b}{ d' } =\frac{n_b-n_a}{ R } \ \ \ \ \ (58)$

Esta é a equação que relaciona a distância entre o objecto e a imagem na refração sobre uma superfície esférica.

Figura 59: Ampliação na refração em superfície esférica. [59] Adaptado

A figura 2 representa um sistema com um objecto ${PQ}$ de altura ${y}$ e a sua imagem ${P'Q'}$ de altura ${y'}$ . A ampliação transversal da imagem é a relação entre as alturas (medidas transversalmente ao eixo principal) da imagem e do objecto.

$\displaystyle k=-\frac{y'}{y} \ \ \ \ \ (59)$

Para este caso, é válida a relação:

$\displaystyle n_a \cdot \sin\theta_a = n_b \cdot \sin \theta_b \ \ \ \ \ (60)$

Analisando os triângulos ${PQV}$ e ${P'Q'V}$ , obtemos as relações:

$\displaystyle \tan \theta_a = \frac{y}{d} \qquad \tan \theta_b = \frac{y'}{d'} \ \ \ \ \ (61)$

Como os raios são paraxiais, é válida a aproximação ${\tan \alpha \approx \sin\alpha\approx \alpha}$ . Logo, as equações 61 e 60 ficam:

$\displaystyle n_a \cdot \theta_a = n_b \cdot \theta_b \ \ \ \ \ (62)$

$\displaystyle \theta_a = \frac{y}{d} \qquad \theta_b = \frac{y'}{d'} \ \ \ \ \ (63)$

Substituindo os resultados da equação 63 na equação 62, obtemos ${n_a \cdot \frac{y}{d} = n_b \cdot \frac{y'}{d'}}$ . Isolando a fracção ${\frac{y'}{y}}$ , obtemos:

$\displaystyle k=-\frac{y'}{y}=-\frac{n_a \cdot d'}{n_b \cdot d} \ \ \ \ \ (64)$

Está é a ampliação transversal na refração numa superfície esférica.

Podemos ver assim que, quando observamos um corpo qualquer sobre uma superfície de separação esférica, além de uma sensação de proximidade ou afastamento, podemos também ter a ilusão de que o objecto tem um tamanho transversal maior ou menor do que o real. É o caso do peixe no aquário. a ampliação da imagem vai depender da posição do objecto e do observador, bem como dos índices de refração dos meios onde estes se encontram.

— Referências Bibliográficas —

[1] Lilia Coronato Courrol & André de Oliveira Preto. APOSTILA TEÓRICA: ÓPTICA TÉCNICA I, FATEC-SP , [s.d.].
[2] Jaime Frejlich. ÓPTICA: TRANSFORMAÇÃO DE FOURIER E PROCESSAMENTO DE IMAGENS, Universidade Federal de Campinas – SP, [2010].
[3] Sérgio C. Zilio. ÓPTICA MODERNA: FUNDAMENTOS E APLICAÇÕES, [2010].
[4] Renan Schetino de Souza. ÓPTICA GEOMÉTRICA, [2012].
[5] Hugh D. Young & Roger Freedman. FÍSICA IV: ÓPTICA E FÍSICA MODERNA, [2009].
[6]Hugh D. Young & Roger Freedman. FÍSICA III: ELECTROMAGNETISMO, [2009].
[7] Julião de Sousa Leal. TRABALHO DE FIM DE CURSO: MANUAL DE ÓPTICA, FACULDADE DE CIÊNCIAS DA UNIVERSIDADE AGOSTINHO NETO, [s.d.]

Aplicação das equações diferenciais de primeira ordem.Corpos em queda

02/24/2016 4:15 pm / 1 comentário em Aplicação das equações diferenciais de primeira ordem.Corpos em queda

— 3.4. Corpos em queda —

Para construir um modelo matemático do movimento de um corpo em um campo de força, em geral iniciamos com a segunda lei do movimento de Newton.Lembre-se da física elementar que a primeira lei do movimento de Newton estabelece que o corpo permanecera em repouso ou continuara movendo-se a uma velocidade constante, a não ser que esteja agindo sobre ele uma força externa.Em cada caso, isso equivale a dizer que quando a soma das forças,isto é, a força resultante, que age sobre sobre o corpo for diferente de zero, essa força resultante será proporcional a aceleração ou mais precisamente:

$\displaystyle F=\sum F_{r}=m\cdot a \ \ \ \ \ (1)$

onde ${m}$ é a massa do corpo.

Suponha agora que uma pedra seja jogada para acima do topo de um prédio, conforme a figura ${1}$ .

Figura 1:Corpos em queda

Qual é a posição ${s(t)}$ da pedra em relação ao chão no instante ${t}$ ?A aceleração da pedra é ${ \frac{d^{2}s}{dt^{2}}}$ .1Se assumirmos como positiva a direção para cima e que nenhuma outra força alem da gravidade age sobre a pedra, obteremos a segunda lei de Newton

$\displaystyle m\frac{d^{2}s}{dt^{2}}=-mg \quad ou \quad \frac{d^{2}s}{dt^{2}}=-g \ \ \ \ \ (2)$

Em outras palavras, a força resultante é simplesmente o peso da pedra próximo a superfície da terra,ou seja:

$\displaystyle F=F_{1}=-P \ \ \ \ \ (3)$

Lembre-se de que a magnitude do peso é ${P=m\cdot g}$ , onde ${g}$ é a aceleração de gravidade.O sinal de subtração foi usado em (2), pois o peso da pedra é uma força dirigida par baixo, oposta a direção positiva.Se a altura do prédio é ${s_{0}}$ e a velocidade inicial da pedra é ${v_{0}}$ , então ${s}$ é determinada, com base no problema de valor inicial de segunda ordem

$\displaystyle \frac{d^{2}s}{dt^{2}}=-g, \quad s(0)=s_{0}, \quad s\prime(0)=v_{0} \ \ \ \ \ (4)$

Embora não estejamos dando enfaze a resolução das equações obtidas, note que a equação ${(4)}$ pode ser resolvida integrando-se a constante ${-g}$ duas vezes em relação a t.As condições iniciais determinam duas constante de integração.Podemos obter a solução de ${(4)}$ como a fórmula

$\displaystyle s(t)=-\dfrac{1}{2}gt^{2}+v_{0}t+s_{0} \ \ \ \ \ (5)$

— 3.4.1. Corpos em queda e a resistência do ar —

Antes dos famosos experimentos de Galileu na torre inclinada de Pisa, acreditava-se que os objetos mais pesados em queda livre, como uma bala de canhão, caiam com uma aceleração maior do que a de objetos mais leves, como uma pena.Obviamente, uma bala de canhão e uma pena , quando largadas simultaneamente da mesma altura, caem a taxas diferentes, mas isso não se deve ao fato de a bala de canhão ser mais pesada.A diferença das taxas é devida a resistência do ar.A força de resistência do ar foi ignorada no modelo dado em ${(4)}$ .Sob algumas circunstancias, um corpo em queda com massa ${m}$ , como uma pena com baixa densidade e formato irregular, encontra uma resistência do ar proporcional a sua velocidade instantânea ${v}$ .Se nessas circunstancias, tomarmos a direção positiva como orientada para baixo, a força resultante que age sobre a massa será dada por

$\displaystyle F=F_{1}+F_{2}=mg-kv \ \ \ \ \ (6)$

onde o peso ${F_{1}=mg}$ do corpo é a força que age na direção positiva e a resistência do ar ${ F_{2}=-kv }$ é uma força chamada amortecimento viscoso que age na direção oposta ou para cima.Veja a figura ${2}$ .

Figura 2:Corpos em queda com resistência do ar

Agora, como a velocidade ${v}$ esta relacionado com a aceleração ${a}$ atraves de ${a=\frac{dv}{dt}}$ , a segunda lei de Newton torna-se

$\displaystyle F=m\cdot a =m\cdot \frac{dv}{dt} \ \ \ \ \ (7)$

substituindo a equação ${(6)}$ em ${(7)}$ obtemos a equação diferencial de primeira ordem para a velocidade ${v(t)}$ do corpo no instante ${t}$ .

$\displaystyle m\frac{dv}{dt}=mg-kv \ \ \ \ \ (8)$

onde ${k}$ é uma constante de proporcionalidade positiva.

como a velocidade inicial do objeto é ${v_{0}}$ , um modelo para a velocidade do corpo que cai se expressa mediante o problema de com valor inicial:

$\displaystyle m\frac{dv}{dt}=mg-kv, \quad v(0)=v_{0} \ \ \ \ \ (9)$

a equação ${(9)}$ é uma equação diferencial linear,ao resolvermos, obtemos:

$\displaystyle v(t)=\dfrac{mg}{k}+\left(v_{0}-\dfrac{mg}{k}\right)e^{-kt/m} \ \ \ \ \ (10)$

considerando ${s=0 }$ quando ${t=0}$ podemos determinar a equação de movimento do objeto integrando ${v=\frac{ds}{dt}}$ em relação a ${t}$ .Assim obtemos

$\displaystyle s(t)=\int v(t)dt=\int\left[\dfrac{mg}{k}+\left(v_{0}-\dfrac{mg}{k}\right)e^{-kt/m}\right]dt$

$\displaystyle s(t)=\dfrac{mg}{k}t-\dfrac{m}{k}\left(v_{0}-\dfrac{mg}{k}\right)e^{-kt/m}+c \ \ \ \ \ (11)$

fazendo ${s=0 }$ e ${t=0 }$ teremos

$\displaystyle 0=-\dfrac{m}{k}\left(v_{0}-\dfrac{mg}{k}\right)+c\Rightarrow c=\dfrac{m}{k}\left(v_{0}-\dfrac{mg}{k}\right)$

Substituindo o valor da constante ${c}$ em ${(11)}$ teremos a equação de movimento:

$\displaystyle s(t)=\dfrac{mg}{k}t+\dfrac{m}{k}\left(v_{0}-\dfrac{mg}{k}\right)(1-e^{-kt/m}) \ \ \ \ \ (12)$

Exemplo 1 Um objeto que pesa ${4}$ N cai desde uma grande altura partindo do repouso.Se o ar exerce uma resistência de ${\frac{1}{2}v}$ N, onde ${v}$ é a velocidade em m/s,figura 3.Achar a velocidade ${v(t)}$ e a distancia percorrida ${s(t)}$ no instante de tempo ${t}$ .

Solução:Consideremos a direção positiva para baixo.

Figura 3:Corpo em queda do exemplo 1

De acordo a segunda Lei de Newton temos:

$\displaystyle m\dfrac{dv}{dt}=F_{1}-F_{2}$

onde ${m=\frac{P}{g}=\frac{4}{32}=\frac{1}{8}, \quad F_{1}=P=4N, \quad F_{2}=\frac{1}{2}v N}$

substituindo teremos a equação diferencial

$\displaystyle \dfrac{1}{8}\dfrac{dv}{dt}=4-\dfrac{1}{2}v \Rightarrow \dfrac{dv}{dt}=32-4v$

separando as variáveis e integrando temos:

$\displaystyle \int\dfrac{dv}{8-v}=\int4dt \Rightarrow -\ln(8-v)=4t+C_{1}$

usando a condição ${v(0)=0,}$ teremos ${C_{1}=-\ln 8}$ .logo, ao substituir este valor de ${C_{1}}$ e isolando ${v}$ temos:

$\displaystyle v(t)=8(1-e^{-4t})$

Para achar ${s(t)}$ resolve-se o problema de valor inicial:

$\displaystyle v(t)=\dfrac{ds}{dt}=8(1-e^{-4t}); \quad s(0)=0$

separando as variáveis e integrando, obtemos:

$\displaystyle s(t)=8(t+\dfrac{1}{4}e^{-4t})+C_{0}$

usando a condição inicial ${s(0)=0}$ , temos ${C_{0}=-2}$ .Portanto

$\displaystyle s(t)=8(t+\dfrac{1}{4}e^{-4t})-2$

Exemplo 2 Um objeto que pesa ${30}$ N se deixa cair desde uma altura de ${40}$ m, com uma velocidade inicial de ${3m/s}$ .Suponhamos que a resistência do ar é proporcional a velocidade do corpo.Se sabe que a velocidade limite deve ser de ${40m/s}$ .Encontrar:

a velocidade depois de ${8 }$ segundos;
a expressão para a posição do corpo no instante de tempo ${t}$ ;

Solução:De acordo a segunda Lei de Newton, temos:

$\displaystyle m\dfrac{dv}{dt}=mg-kv$

onde ${P=30N \Rightarrow m=\frac{P}{g}=\frac{30}{9,8}\cong 3kg}$

temos que ${v_{lim}=40 m/s}$ onde ${v_{lim}=\frac{mg}{k}}$ ;então:

$\displaystyle k=\dfrac{mg}{v_{lim}}=\dfrac{30}{40} \Rightarrow k=\dfrac{3}{4}Ns/m$

substituindo esses valores na segunda Lei de Newton temos:

$\displaystyle \dfrac{dv}{dt}+\dfrac{1}{4}v=10$

resolvendo a equação diferencial linear teremos:

$\displaystyle v=C_{1}e^{-t/4}+40$

com a condição inicial ${v(t)=v_{0}\Rightarrow v(0)=3m/s}$ , temos:

$\displaystyle 3=C_{1}+40 \Rightarrow C_{1}=-37$

então, a velocidade em qualquer instante de tempo ${t}$ é:

$\displaystyle v=-37e^{-t/4}+40$

Para ${t=8s}$ temos:

$\displaystyle v(t)=-37e^{-8/4}+40 \Rightarrow v=35m/s$

Para encontrar a posição do corpo temos ${v=\frac{ds}{dt}}$ , então:

$\displaystyle \dfrac{ds}{dt}=-37e^{-y/4}+40$

a equação acima é uma equação de variáveis separáveis, resolvendo teremos como solução:

$\displaystyle s(t)=148e^{-t/4}+40t+C_{2}$

Aplicando a condição inicial ${s(t)=s_{0}\Rightarrow s(0)=0}$ teremos ${C_{2}=-148}$

portanto,

$\displaystyle s(t)=148e^{-t/4}+40t-148$

Aplicação das equações diferenciais de primeira ordem.Circuitos elétricos

02/23/2016 9:41 am / 3 comentários em Aplicação das equações diferenciais de primeira ordem.Circuitos elétricos

— 3.3.Circuitos em série —

Um circuito consiste em um numero qualquer de elementos unidos por seus terminais, com pelo menos um caminho fechado através do qual a carga possa fluir.

Dois elementos estão em serie se:

Possuem somente um terminal em comum(isto é, um terminal de um esta conectado somente a um terminal do outro).
O ponto comum entre os dois elementos não esta conectado a outro elemento percorrido por corrente

Neste artigo, examinaremos dois tipos de circuitos em serie:um circuito compreendendo um resistor e um capacitor e outro circuito formado por um resistor e um indutor.Estes circuitos são denominados, respetivamente, circuitos ${RC}$ e ${RL}$ , e apesar de sua simplicidade tem inúmeras aplicações em eletrónica, comunicações e sistemas de controle.

A análise de circuitos ${RC}$ e ${RL}$ aplicando as leis de Kirchhoff produz equações diferenciais.As equações diferenciais resultantes da analise de circuitos ${RC}$ e ${RL}$ são de primeira ordem, consequentemente, os circuitos são conhecido coletivamente como circuitos de primeira ordem.

Consideremos um circuito em serie contendo somente um resistor e um indutor, a segunda lei de Kirchhoff diz que a soma da queda de tensão no indutor ( ${ L\frac{di}{dt} }$ ) e da queda de tensão no resistor ( ${ iR }$ ) é igual a voltagem ( ${ E(t) }$ ) no circuito.Veja a figura 1;

Figura 1:Circuito em série RL

Logo, obtemos a equação diferencial linear para a corrente ( ${ i(t) }$ ).

$\displaystyle L\dfrac{di}{dt}+Ri=E(t) \ \ \ \ \ (1)$

em que L e R são constante conhecidas como a indutância e a resistência, respetivamente.A corrente é algumas vezes chamada de resposta do sistema.

A queda de potencial em um capacitor com capacitância ${ C }$ é dada por ${\frac{q(t)}{C}}$ , em que q é a carga no apacitor.Então, para o circuito em serie mostrado na figura 2, a segunda lei de Kirchhoff nos dá

$\displaystyle Ri+\frac{1}{C}q=E(t) \ \ \ \ \ (2)$

Figura 2:Circuito em série RC

Mas a corrente ${i}$ e a carga ${q}$ estão relacionados por ${ i=\frac{dq}{dt} }$ , logo, torna-se a equação diferencial linear

$\displaystyle R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t) \ \ \ \ \ (3)$

Exemplo 1 Um circuito ${RL}$ tem uma fem de ${5}$ voltes, uma indutância de ${1}$ henry, uma resistência de ${80}$ ohm e não tem corrente inicial.Determinar a corrente no circuito para qualquer instante de tempo ${t}$ .

Solução:A quantidade de corrente ${i}$ no circuito é:

$\displaystyle \dfrac{di}{dt}+\dfrac{R}{L}i=\dfrac{E}{L}$

sabemos que ${ E=5V ,\quad L=1H, \quad R=80\Omega }$ ,então a equação do circuito será:

$\displaystyle \dfrac{di}{dt}+80i=5$

resolvendo a equação diferencial linear acima temos:

$\displaystyle i=\dfrac{1}{16}+ce^{-80t}$

o exemplo diz que o circuito não tem corrente inicial, ou seja, para ${t=0 \Rightarrow i=0}$ , então: ${ c=-\dfrac{1}{16} }$

assim, a corrente em qualquer instante de tempo ${t}$ é:

$\displaystyle i=\dfrac{1}{16}-\dfrac{1}{16}e^{-80t}\Rightarrow i=\dfrac{1}{16}(1-e^{-80t})$

Exemplo 2 Um circuito ${RC}$ tem uma fem de ${200 \cos 2t}$ volt, uma resistência de ${50}$ ohm e uma capacitância de ${10^{-2}}$ farad. Em t=0 não há carga no condensador.Achar a corrente no circuito no instante ${t}$ .

Solução:A equação para a quantidade de carga electrica ${q}$ é:

$\displaystyle \dfrac{dq}{dt}+\dfrac{1}{RC}q=\dfrac{E}{R}$

sabemos que ${E=(200\cos 2t)V, \quad R=50\Omega, \quad C=10^{-2}F}$ , então a equação do circuito será:

$\displaystyle \dfrac{dq}{dt}+2q=4 \cos2t$

resolvendo a equação diferencial linear acima temos:

$\displaystyle q= \cos 2t + \sin 2t + ce^{-2t}$

Para ${t=0, \quad q=0;}$ então: ${c=-1}$

Para determinarmos a corrente temos que ter em mente que:

$\displaystyle i=\dfrac{dq}{dt}$

e uma vez obtida a carga, podemos encontrar a corrente:

$\displaystyle i=\dfrac{dq}{dt}=-2 \sin 2t + 2 \cos 2t + 2e^{-2t}$

Conheça a física dos óculos. Lentes. Características principais.

02/22/2016 10:34 pm / 2 comentários em Conheça a física dos óculos. Lentes. Características principais.

— 2.7.10. Lentes —

A possibilidade de observar a imagem dos objectos em um tamanho muitas vezes maior que o próprio objecto acabou por marcar um grande passo no desenvolvimento do mundo. A invenção do microscópio óptico e dos telescópios, permitiu ao mundo conhecer outras dimensões microscópicas (células, bactérias, vírus, etc) como astronómicas (galáxias, sistemas solares, etc).

Há certos dispositivos que são usados para aumentar, diminuir ou tornar mais nítida uma imagem. São exemplos destes dispositivos as lupas, microscópios, telescópios, as objectivas (lentes objectivas), etc. Estes dispositivos são, em geral, lentes, ou são constituídos principalmente por lentes.

As lentes acabam assim por ser uma invenção importantíssima para a humanidade. Além das aplicações anteriormente citadas, são ferramenta importante para a maioria dos humanos com deficiência de visão. Uma lente é um dispositivo óptico formado por uma substância transparente, homogénea, limitada por duas superfícies esféricas ou cilíndricas, ou por uma superfície esférica ou cilíndrica e outra plana. Por incrível que pareça, até o fundo de certos copos e garrafões enquadra-se no conceito de lente.

As lentes que aqui vamos estudar são as lentes delgadas, isto é, lentes de espessura muito pequena. Para a nomenclatura das lentes, o critério mais adotado é nomear as faces voltadas para o meio exterior, assinalando em primeiro lugar a face de maior raio de curvatura.

Figura 52 : (a) Lentes convergentes: Lente bi-convexa, lente plano-convexa, lente côncavo-convexa. (b) Lentes divergentes: Lente bi-côncava, lente plano-côncava, lente convexo-côncava.

Uma recta que seja simultaneamente perpendicular a ambas superfícies que limitam a lente é denominada eixo principal da lente. Essa recta passa necessariamente no centro das duas superfícies (no caso em que ambas sejam esféricas ou cilíndricas). O ponto de interceção desta recta (eixo principal) com a lente é denominado centro óptico da lente.

Figura 53: Eixo principal e Centro da Lente.

De acordo com as características das faces, as lentes classificam-se em dois grupos. Consideremos, inicialmente, lentes de vidro (n = 1,5) colocadas no ar (n = 1). Nestes casos, que são os mais comuns, temos:

Lentes cuja espessura vai diminuindo gradualmente do centro para o bordo são chamadas lentes convergentes;
Lentes cuja espessura vai aumentando gradualmente do centro para o bordo são chamadas lentes divergentes.

Figura 54: Representação simbólica da lente: a) Lente divergente. b) Lente convergente. [7]

Para simplificar a representação das lentes na resolução de exercícios e problemas, usaremos a representação simbólica da figura 54 .

Quando os raios luminosos incidem paralelamente ao eixo principal de uma lente convergente, refratam-se no interior da lente e emergem passando por um ponto ${F'}$ a que se dá o nome de foco imagem da lente.

Numa lente divergente, os raios paralelos ao eixo principal refratam-se no interior e saem para fora da lente (emergem) de modo a que os seus prolongamentos passam por um ponto ${F'}$ , denominado foco imagem da lente. O foco imagem de uma lente convergente é real e o de uma lente divergente é virtual.

Figura 55: Foco imagem: a) Lente convergente. b) Lente divergente. [4] Adaptado

Tanto nas lentes convergentes como nas lentes divergentes, há, sobre o eixo principal um ponto simétrico ${F}$ do foco imagem ${F'}$ em relação ao centro óptico ${0}$ da lente. Este ponto ${F}$ chama-se foco objecto. Os raios que passam pelo foco objecto e atingem a lente convergente, emergem paralelamente ao eixo principal. No caso de uma lente divergente, os raios incidentes cujos prolongamentos passam pelo foco objecto ${F}$ refratam-se no interior e saem da lente paralelamente ao seu eixo principal.

Figura 56: Foco objecto: a) Lente convergente. b) Lente divergente. [4] Adaptado.

Se considerarmos um conjunto de raios incidentes paralelos a um eixo suplementar ${S0}$ da lente convergente (que é um eixo constituído por uma recta que passa pelo centro óptico ${0}$ inclinada em relação ao eixo principal da lente), eles passam pelo foco secundário ${S'}$ . O conjunto desses focos secundários constituem o plano focal imagem.

Figura 57: Plano focal: a) Lente convergente. b) Lente divergente. [4] Adaptado

Um parâmetro muito importante para uma lente é a distância focal. A distância focal ${f}$ de uma lente delgada é a distância entre o centro óptico ${0}$ da lente e o seu foco imagem ${F'}$ ou foco objecto ${F}$ . Vale lembrar que, para lentes delgadas, a distância entre o centro e o foco objecto é igual a distância entre o centro e o foco imagem. Mais adiante, demonstraremos a seguinte fórmula:

$\displaystyle \frac{1}{f}=(n_{21}-1)\cdot(\frac{1}{R_1}+\frac{1}{R_2})\ \ \ \ \ (49)$

Em que:

${n_{21}}$ – Índice de refracção relativo do meio de que é feita a lente com respeito ao meio circundante.
${R_1}$ e ${R_2}$ são respectivamente os raios de curvatura das faces anterior e posterior da lente.

A convenção de sinal para ${R_1}$ e ${R_2}$ é:

Se a face é convexa: ${R>0}$
Se a face é côncava: ${R<0}$
Se a face é plana: ${R=\infty}$

Se o valor da distância focal obtido no cálculo for positivo ( ${f > 0}$ ), a lente é convergente. Se o valor da distância focal for negativo ( ${f <0}$ ) a lente é divergente.

A convergência de uma lente ou potência focal é ao inverso da distância focal da lente.

$\displaystyle D= \frac{1}{f} \ \ \ \ \ (50)$

No sistema internacional de unidades (SI) a distância focal é expressa em metros, então, a convergência da lente é expressa em dioptrias ( ${D}$ ou ${dp}$ ).

A convergência de uma lente pode ser positiva ou negativa.

Convencionalmente:

Para as lentes convergentes, a convergência é positiva: ${f >0}$
Para as lentes divergentes, a convergência é negativa: ${f<0}$

É claro que quanto menor for a distância focal, mais acentuadamente a lente refrata os raios incidentes reunindo-os ou dispersando-os, e maior é o valor absoluto da convergência.

— Referências Bibliográficas —

Luso Academia no Facebook

02/21/2016 10:00 am / Deixe um comentário

Neste novo ano queremos agradecer a todos os nossos leitores que têm apoiado o Luso Academia com as suas visitas e partilhas diárias. Prometemos que vamos continuar a trabalhar com o mesmo esforço e dedicação que temos mostrado até agora e trazer mais matérias que possam ajudar os estudantes pela lusofonia a concluírem os seus estudos.

Queremos também aproveitar para referir mais uma vez que para além do nosso blog temos ainda uma página de facebook: Luso Academia e gostaríamos de ter lá o vosso like e que também a partilhassem pelos vossos amigos para que possamos chegar a um número maior de leitores e aumentar o nosso impacto.

Para finalizar queremos somente dizer que este projecto vive não só das vossas visitas e partilhas mas também dos vossos comentários. Por isso não tenham vergonha e digam de vossa justiça nos nossos artigos para que possamos ajudar mais e melhor quem nos lê.

Aplicações das equações diferenciais de primeira ordem.

02/17/2016 12:30 am / Deixe um comentário

— 3. Aplicações das equações diferenciais de primeira ordem. —

Em ciências, engenharia, economia e ate mesmo em psicologia, frequentemente desejamos descrever ou modelar o comportamento de algum sistema ou fenómeno em termos matemáticos.

A construção de um modelo matemático de um sistema começa com:

a identificação das variáveis responsáveis pela variação do sistema.Podemos a principio optar por não incorporar todas essa variáveis no modelo.Nesta etapa, estamos especificando o nível de resolução do modelo.
a elaboração de um conjunto de hipóteses razoáveis sobre o sistema que estamos tentando descrever.As hipóteses também incluem algumas leis empíricas que são aplicáveis ao sistema.

A estrutura matemática de todas essas hipóteses, ou o modelo matemático do sistema, é muitas vezes uma equação diferencial ou um sistema de equações diferenciais.Esperamos que um modelo matemático razoável do sistema tenha uma solução que seja consistente com o comportamento conhecido do sistema.Porem se as predições obtidas pela solução forem pobres, poderemos elevar o nível de resolução do modelo ou levantar hipóteses alternativas sobre o mecanismo de mudança do sistema.As etapas do processo de modelagem são então repetidas, conforme disposto no diagrama da Figura 1.

Figura 1:Diagrama para criar modelos matemáticos

Naturalmente, aumentando a resolução aumentaremos a complexidade do modelo matemático e, assim, a probabilidade de não conseguirmos obter uma solução explicita.

Um modelo matemático de um sistema físico frequentemente envolve a variável tempo t.Uma solução do modelo oferece então o estado do sistema; em outras palavras, os valores da variável (ou variáveis) para valores apropriados de t descrevem o sistema no passado, presente e futuro.

— 3.1. Crescimento e decrescimento —

O modelo mais simples de crescimento populacional é aquele em que se supõe que a taxa de crescimento de uma população ${\frac{dx}{dt}}$ é proporcional a população presente naquele instante ${x(t)}$ ,ou seja, quanto mais pessoas houver em um instante t, mais pessoas existirão no futuro. Podemos descrever o problema de encontrar ${x(t)}$ como o problema de valor inicial

$\displaystyle \dfrac{dx}{dt}=kx, \quad x(t_{0})=x_{0}, \quad x=x_{0}e^{kt} \ \ \ \ \ (1)$

onde k é uma constante de proporcionalidade, serve como modelo para diversos fenómenos envolvendo crescimento ou decrescimento

Exemplo 1.Em uma cultura, há inicialmente ${P_{0}}$ bactérias.Uma hora depois, t=1 o numero de bactérias passa a ser ${(3/2)P_{0}}$ .Se a taxa de crescimento é proporcional ao numero de bactérias presentes, determine o tempo necessário para que o numero de bactérias triplique

Solução:Primeiro resolvemos a equação diferencial

$\displaystyle \dfrac{dP}{dt}=kP$

sujeita a ${P(0)=P_{0}}$ .Então, usamos a condição empírica ${P(1)=(3/2)P_{0}}$ para determinar a constante de proporcionalidade k.Resolvendo a equação diferencial acima temos:

$\displaystyle \int \dfrac{dP}{P}=\int kdt\Rightarrow ln P=kt+c$

$\displaystyle P=e^{kt+c} \Rightarrow P(t)=ce^{kt}$

Em ${t=0}$ concluímos que

$\displaystyle P_{0}=ce^{0}=c$

assim, teremos:

$\displaystyle P(t)=P_{0}e^{kt}$

Em ${t=1}$ , temos:

$\displaystyle \frac{3}{2}P_{0}=P_{0}e^{kt}\Rightarrow e^{k}=\frac{3}{2}\Rightarrow k=ln (3/2)\Rightarrow k=0,4055$

A expressão N(t) é portanto

$\displaystyle P(t)=P_{0}e^{0,4055t}$

para encontrar o tempo necessário para que o numero de bactérias seja triplicado, resolvemos:

$\displaystyle 3P_{0}=P_{0}e^{0,4055t}\Rightarrow t=\dfrac{ln 3}{0,4055}\Rightarrow t=2,71horas$

Figura 2:Tempo que o numero de bactérias triplica

Como mostrado na Figura 3, a função exponencial ${e^{kt}}$ cresce com o tempo quando ${k>0}$ , e decresce quando ${k<0.}$ Logo, problemas que descrevem crescimentos, como população, bactéria ou mesmo capital, são caraterizados por um valor positivo de k; por outro lado, problemas, como desintegração radioativa, conduzem a um valor negativo de k.

Figura 3:Crescimento ${k>0}$ e decrescimento ${k<0.}$

Exemplo 2.A população de uma cidade cresce a uma taxa proporcional á população em qualquer tempo.Sua população inicial de 500 habitantes aumenta ${15^{o}/_{o}}$ em 10 anos.Qual será a população em 30 anos?

Solução:Primeiro resolvemos a equação diferencial

$\displaystyle \dfrac{dP}{dt}=kP, \quad P(0)=500$

Resolvendo a equação diferencial acima obtemos:

$\displaystyle P(t)=ce^{kt}$

Aplicando a condição inicial

$\displaystyle P(0)=500$

na equação acima temos:

$\displaystyle 500=ce^{k0}\Rightarrow c=500$

Então,

$\displaystyle P(t)=500e^{kt}$

sabemos que população inicial de 500 habitantes aumenta ${15^{o}/_{o}}$ ,ou seja, 75 habitantes em 10 anos,isto quer que depois de 10 anos a cidade tem 575 habitantes.logo,

$\displaystyle P(10)=575\Rightarrow 575=500e^{k10}\Rightarrow k=\frac{1}{10}ln 1.15$

já temos o valor de k, agora podemos determinar a população em 30 anos:

$\displaystyle P(30)=500e^{30(\frac{1}{10}ln 1.15)}\Rightarrow P(30)=760$

em 30 anos a cidade terá 760 habitantes.

— 3.2. Resfriamento —

A lei de resfriamento de Newton diz que a taxa de variação de temperatura ${T(t)}$ de um corpo em resfriamento é proporcional a diferença entre temperatura do corpo ${T}$ e a temperatura constante ${T_{m}}$ do meio ambiente, isto é:

$\displaystyle \dfrac{dT}{dt}=k(T-T_{m}) \ \ \ \ \ (2)$

em que k é uma constante de proporcionalidade.

Exemplo 3.Quando um bolo é retirado do forno, sua temperatura é de 300ºF.Tres minutos depois, sua temperatura passa para 200ºF.Quanto tempo levara para sua temperatura chegar a 75graus, se a temperatura do meio ambiente em que ele foi colocado for de exatamente 70ºF?

Solução:Com base a lei de resfriamento de Newton temos:

${T_{m}=70^{o}F}$ é a temperatura do meio ambiente;
T é a temperatura do bolo;

Devemos então resolver o problema de valor inicial

$\displaystyle \dfrac{dT}{dt}=k(T-T_{m}), \quad T(0)=300^{o}F$

e determinar o valor de K para que ${T(3)=200^{o}F.}$

A equação acima é linear e separável.Separando as variáveis, temos

$\displaystyle \dfrac{dT}{T-70}=kdt\Rightarrow ln |T-70|=kt+c_{1}$

$\displaystyle T-70=e^{kt+c_{1}}\Rightarrow T=70+c_{2}e^{kt}$

quando ${t=0, \quad T=300}$ .substituindo na ultima expressão teremos:

$\displaystyle 300=70+c_{2}e^{k0}\Rightarrow c_{2}=230$

Então,

$\displaystyle T=70+230e^{kt}$

agora estamos em condições para determinar o valor de k para ${T(3)=200}$ , de modo que teremos

$\displaystyle 200=70+230e^{k3}\Rightarrow e^{k3}=\dfrac{130}{230}\Rightarrow k=\frac{1}{3}ln \frac{13}{23}=-0,191018$

Então,

$\displaystyle T=70+230e^{-0,191018t}$

com base a ultima equação estamos em condições para achar o tempo ( ${t}$ ) que o bolo levara para atingir 75 graus ( ${T=75}$ ), fazendo:

$\displaystyle 75=70+230e^{-0,191018t}\Rightarrow e^{-0,191018t}=\dfrac{75-70}{230}\Rightarrow -0,191018t=ln \dfrac{5}{230}$

$\displaystyle t=20,13minutos$

Exemplo 4.Um termómetro é retirado de dentro de uma sala e colocado do lado de fora, em que a temperatura é de ${5^{0}C}$ .Após 1 minuto, o termómetro marcava 55ºC; após 5 minutos, 30ºC.Qual é a temperatura da sala? Solução:se

${T_{m}=5^{o}C}$ é a temperatura do ar;
${T}$ é a temperatura da sala;

então:

$\displaystyle \dfrac{dT}{dt}=k(T-5) \Rightarrow T=5+c_{2}e^{kt}$

se ${T(1)=55^{o}C}$ teremos

$\displaystyle 55=5+c_{2}e^{k1}\Rightarrow c_{2}e^{k}=50\Rightarrow c_{2}=50e^{-k}$

e se ${T(5)=30^{o}C}$ teremos

$\displaystyle 30=5+c_{2}e^{k5}\Rightarrow c_{2}e^{5k}=25$

substituindo ${c_{2}=50e^{-k}}$ na ultima expressão teremos

$\displaystyle 50e^{-k}e^{5k}=25\Rightarrow e^{4k}=\dfrac{25}{50}\Rightarrow k=-\dfrac{1}{4}ln 2$

o valor de ${c_{2}}$ será:

$\displaystyle c_{2}=50e^{-k}=50e^{-(-\frac{1}{4}ln 2 )}\Rightarrow c_{2}=59,4611$

então,

$\displaystyle T=5+59,4611e^{-\frac{1}{4}tln 2}$

agora podemos determinar a temperatura da sala no instante inicial, substituindo ${t=0}$ na equação acima,onde:

$\displaystyle T(0)=64,4611^{o}C$

Como a Física explica o arco-íris? Dispersão da luz. Prisma.

02/16/2016 8:36 pm / 1 comentário em Como a Física explica o arco-íris? Dispersão da luz. Prisma.

— 2.7.14. Dispersão da luz. Prisma. —

O arco-íris é um fenómeno natural muito bonito, que suscita a curiosidade de muitos. Como se formam aquelas cores? De onde vêm?

A resposta desta questão está na dispersão da luz. Dispersão da luz é o fenómeno da separação de uma onda luminosa em várias componentes espectrais.

Como estudamos, existe luz monocromática (com uma única componente espectral, ou seja, um único comprimento de onda) e luz policromática (com várias componentes espectrais). A luz da maioria das fontes ordinárias (lâmpadas incandescentes, lâmpadas fluorescentes, lâmpadas de descarga, luz solar, luz emitida por aquecimento dos corpos, etc.) são policromáticas. No nosso dia-a-dia, só a luz provenientes de alguns LED´s como vermelhos, azuis, amarelos e verdes e a luz proveniente de um laser são monocromáticas.

Como estudamos também, no item em que falamos de índice de refração, a forma como feixes de diferentes comprimentos de onda passa por um material é ligeiramente diferente, ou seja, ao refratar-se numa dada superfície de separação, os raios de comprimentos de onda diferente passarão de modo diferente. Mesmo que dois feixes com comprimento de onda diferente incidam sobre uma superfície de separação com o o mesmo ângulo de incidência, os ângulos de refração serão minimamente diferentes. Essa diferença ocorre porque o índice de refração de um material não é fixo para todo tipo de radiações, ou seja, radiações diferentes, têm, para o mesmo material, índice de refração diferente. É como se a oposição que o material oferece a passagem da luz variasse de acordo com o comprimento de onda da mesma.

Alguns sistemas acentuam esta diferença e outros não. Um dos sistemas que acentua esta diferença é o prisma. Isaac Newton usou-o para mostrar que a luz branca é policromática, provocando a dispersão da luz branca num prisma, observando assim o seu espéctro.

Figura 48: Prisma. [4]

Um bloco de material transparente e homogéneo com duas faces laterais lisas e inclinadas como indica a figura 48, é um prisma.

Figura 49: Dispersão no prisma.[4]

Observe a figura 49. Quando um raio de luz policromático, por exemplo a luz branca, incide num prisma com o certo ângulo, sendo que os diversos comprimentos de onda sofrem refração como se o índice de refração do material de que é feito o prisma fosse diferente para cada um deles, os ângulos com que eles saem do prisma serão então diferentes, saindo cada um numa direcção relativamente diferente. Se colocarmos um anteparo branco no caminho do feixe que sai do prisma, poderemos observar o espéctro da cor branca (arco-íris).

Em geral, a extremidade mais delgada da gota de água apresenta formato idêntico ao de um prisma, logo, quando a luz incide sobre as gotas de água, acontece algo idêntico ao que acontece no prisma; só que, tal como no prisma, a dispersão só é observada para certos ângulos.

Figura 50: Dispersão da luz na gota de água. Arco-íris. [4]

No caso mais simples de passagem da luz no prisma, em que a luz incide sobre uma das faces do prisma e refrata-se na face imediatamente a seguir (relativamente a passagem do raio), as relações entre os diversos ângulos podem ser deduzidas.

Figura 51: Dedução das fórmulas do prisma.

Seja um raio luminoso que fica no plano de uma certa secção transversal do prisma ${RST}$ e que incide sobre a aresta ${RS}$ sob o ângulo de incidência ${\alpha_1}$ . Este raio é refratado no interior do prisma com um ângulo ${\beta_1}$ e, ainda no interior do prisma, incide sobre a face ${RT}$ com um ângulo ${\beta_2}$ e refrata-se novamente no ar sob o ângulo de emergência ${\alpha_2}$ . Consideramos ${n}$ o índice de refracção do meio de que é feito o prisma em relação ao meio ambiente e ${A}$ o ângulo no vértice superior do prisma (vértice oposto á base do triângulo, ver figura 51).

Na figura, ${c}$ e ${d}$ são as normais às superfícies ${RS}$ e ${RT}$ , respectivamente. ${\delta}$ é o desvio que o prisma provoca no raio incidente, ou seja, a separação angular entre o raio incidente e o raio emergente.

No triângulo ${MOP}$ , aplicando o teorema dos ângulos internos de um triângulo, podemos obter para o ângulo ${x}$ :

$\displaystyle x=180^0-\beta_1-\beta_2 \ \ \ \ \ (45)$

No quadrilátero ${MROP}$ , como as rectas ${c}$ e ${d}$ são normais às superfícies ${RS}$ e ${RT}$ , então os seus ângulos internos são ${90^0}$ . Logo, aplicando o teorema dos ângulos internos de um quadrilátero, teremos: ${A+90^0+90^0+x=360^0\Rightarrow A=180^0-x}$ . Substituindo ${x}$ pela equação 45, obtemos:

$\displaystyle A=\beta_1+\beta_2 \ \ \ \ \ (46)$

Analisando o triângulo ${MNP}$ , de acordo com o teorema de ângulos opostos em rectas que se cruzam, obtemos ${w=\alpha_1-\beta_1}$ e ${z=\alpha_2-\beta_2}$ . Logo, ${y=180^0-w-z=180^0-\alpha_1+\beta_1-\alpha_2+\beta_2}$ . Substituindo a equação 46, obtemos:

$\displaystyle y=180^0-\alpha_1-\alpha_2+A \ \ \ \ \ (47)$

Como ${y}$ e ${\delta}$ são suplementares, então ${\delta=180^0-y}$ . Substituindo ${y}$ pelo valor obtido na equação 47, e efectuando as devidas simplificações, obtemos:

$\displaystyle \delta=\alpha_1+\alpha_2-A \ \ \ \ \ (48)$

Os ângulos ${\alpha_1}$ e ${\beta_1}$ , bem como os ângulos ${\alpha_2}$ e ${\beta_2}$ estão relacionados pela lei de Snell-Descartes para a refração (ar-material do prisma, para o primeiro caso, e material do prisma-ar para o segundo caso).

Se o prisma estiver imerso na água ou noutra substância qualquer, devemos apenas mudar o índice de refração relativo do material de que é feito o prisma, ou seja, ${n}$ .

Vale lembrar que podem haver situações em que a luz, na segunda superfície ( ${RT}$ , no nosso caso) sofra reflexão total interna, e o raio emergente saia num outra face. Nestes casos, estas equações não se aplicam, sendo necessário aplicar raciocínios idênticos para deduzir as suas equações.

Está a gostar da Abordagem? Veja também:

— Referências Bibliográficas —

Como a Física explica a deformação da imagem dos corpos submersos na água?

02/13/2016 3:43 am / 1 comentário em Como a Física explica a deformação da imagem dos corpos submersos na água?

— 2.7.12. Refração em Dióptro plano —

Dióptro plano é o conjunto de dois meios homogéneos e transparentes, separados por uma superfície plana (ex: a água tranquila de um lago e o ar, ar e um objecto de vidro de superfície plana, etc.). Quando estamos fora da água e observamos um peixe que está dentro da água, temos a sensação de que o peixe se encontra a uma certa distância, mas se sentarmos apanha-lo, notamos que há uma diferença entre a posição real onde o peixe realmente se encontra e a posição da imagem deste peixe que nós vemos. O mesmo ocorre quando estando dentro da água (por exemplo de uma piscina), observamos uma pessoa que está na margem, acima da superfície livre da água.

Este fenómeno é chamado de profundidade aparente e é explicado através da lei de Snell-Descartes, quando se analisa a refração em um dióptro plano.

Um peixe dentro da água difunde luz em todas as direcções. Parte da luz difundida refrata-se ao atingir a superfície de separação dos meios água-ar.

Figura 45: Imagem observada num dióptro plano. [5]

Como a água é mais refringente que o ar (mais densa opticamente), os raios refratados da água para o ar afastam-se da normal e podem ser captados por um observador; este, em vez de ver directamente o objecto na posição ${P}$ , vê a sua imagem, em ${P'}$ , na intercecção dos prolongamentos dos raios refratados (imagem virtual do objecto real ${P}$ ). O observador fica com a sensação de que o objecto (no caso, o peixe) está mais próximo, quando na realidade ele está mais distante. Lembre-se que num sistema óptico qualquer, nós vemos a imagem produzida por este sistema óptico e não o objecto propriamente dito.

Figura 46: Profundidade aparente. [7]

Podemos estabelecer a relação entre profundidade real e profundidade aparente.

Na figura 46, o triângulo ${API}$ , o ângulo interno do vértice A é ${i_1}$ e no triângulo ${A'PI}$ o ângulo no vértice ${A'}$ é ${i_2}$ . As suas tangentes são ${tg (i_1) =\frac{PI}{AP}=\frac{x}{d}}$ e ${tg (i_2) =\frac{PI}{A'P}=\frac{x}{d'}}$ . Dividindo estas duas relações, fica ${ \frac{tg (i_1)}{tg (i_2)} =\frac{d'}{d}}$ . Para observadores muito próximos da normal, ${i_1}$ e ${i_2}$ são muito pequenos , logo é válida a aproximação ${tg (i_1) \approx sen (i_1) \approx i_1}$ . O mesmo ocorre com ${i_2}$ . Logo a relação pode ser escrita por ${ \frac{tg (i_1)}{tg (i_2)} = \frac{sen (i_1)}{sen (i_2)} =\frac{n_2}{n_1} = \frac{d'}{d}}$ :

Neste caso a relação entre a profundidade real e a profundidade aparente será:

$\displaystyle d=\frac{n_2}{n_1} . d' \ \ \ \ \ (39)$

Observamos assim que a profundidade aparente ${d'}$ é diferente da profundidade real ${d}$ , podendo ser maior ou menor.

A profundidade aparente será menor do que a profundidade real se o meio no qual se situa o observador tiver um índice de refração menor do que o índice de refração do meio onde se encontra o objecto. Nestes casos o observador terá a sensação de que o objecto está mais próximo do que a sua posição real. Um exemplo disto é uma pessoa, na fora do lago que observa um peixe no lado.

De modo análogo, a profundidade aparente será maior do que a profundidade real quando o observador se encontrar num meio que tenha o índice de refração maior do que o índice de refração do meio onde se encontra o objecto. Neste caso, o observador terá a sensação de que o objecto está mais distante do que a sua posição real. Um exemplo disso é o caso de uma pessoa no interior da água que observa algo ou alguém fora da água.

Este conceito tem muitas consequências, com várias aplicações no dia-a-dia. Se quiseres atingir um peixe na água com um arpão, por exemplo, não deves atira-lo na direção da imagem que vês, mas sim um pouco abaixo dela. Caso contrário, falharás o alvo.

— 2.7.13. Superfície de faces paralelas —

Quando falamos de lâmina de faces paralelas (ou superfície de faces paralelas), falamos de uma placa de material transparente e homogénea, limitada por duas faces lisas, planas e paralelas.

Vários sistemas ópticos usados no nosso dia-a-dia são lâminas de faces paralelas, mas um exemplo mais simples são os vidro que constituem as janelas vidradas, muito comuns, nos dias de hoje.

Ao observarmos perpendicularmente sobre a lâmina, não ocorre nenhuma modificação na imagem, mas quando observamos obliquamente sobre ela, podemos notar uma certa deformação na imagem do objecto. Esta deformação será mais notada quanto maior for o índice de refração do material que constitui a lâmina, bem como quanto maior for a espessura da lâmina.

A deformação também aumenta com o aumento do ângulo de visualização. Este experimento pode ser facilmente realizado. Arranje um bloco (em forma de paralelepípedo) de material transparente (vidro, plástico ou outro). Caso não encontre o paralelepípedo, pode usar um material com outro formato qualquer, desde que tenha duas faces paralelas. Coloque um papel com letras num das faces e observe pela outra. Em seguida, vá inclinando a lâmina (em relação as letras e observa o que acontece com a imagem.

Figura 47: Trajecto de raios luminosos numa lâmina de faces paralelas. [7]

Na figura, a espessura da lâmina é designada por ${e}$ , o seu índice de refracção relativo com respeito ao meio circundante (o ar) é ${n}$ ( ${n>1}$ ). O raio incidente ${SD}$ é refratado pela face superior da lâmina passando de no caminho indicado pelo segmento ${DF}$ e sai fora da lâmina no raio indicado por ${FR}$ . Segundo a lei de Snell-Descartes, para a refracção pela face superior, temos:

$\displaystyle 1. sen( i_1) = n . sen (r_1) \ \ \ \ \ (40)$

e para a refracção pela face inferior, temos:

$\displaystyle n. sen (r_2) = 1. sen (i_2) \ \ \ \ \ (41)$

Ora, como se vê na figura, os ângulos ${r_1}$ e ${r_2}$ são iguais. Logo: ${ r1 = r2 = r}$ Substituindo esta igualdade nas equações 40 e 41, obtemos que:

$\displaystyle i_1=i_2=i \ \ \ \ \ (42)$

Ao atravessar a lâmina de faces paralelas o raio luminoso não muda de direcção de propagação. O raio emergente é paralelo ao raio incidente. Apesar de o raio emergente ser paralelo ao raio incidente, mas a imagem observada não é (em geral) igual ao objecto. Suponhamos que o objecto luminoso ${S}$ emite raios pouco inclinados em relação a normal das faces da lâmina. A imagem de ${S}$ criada pela lâmina será ${S'}$ . O deslocamento da imagem em relação ao objecto é ${\delta = SS'}$ . O afastamento entre os dois raios paralelos (incidente ${SD}$ e emergente ${FR}$ ), ou seja, o deslocamento transversal do raio emergente em relação ao raio incidente é igual a ${d}$ . A relação entre estes parâmetros poderá ser deduzida.

Consideremos a figura 47. O triângulo ${FGD}$ , recto no ângulo sob o vértice ${G}$ , o ângulo interno do vértice ${F}$ será ${i-r}$ . O seu seno será ${sen (i-r) =\frac{DG}{DF}=\frac{d}{DF}}$ . Então:

$\displaystyle DF=\frac{d}{sen(i-r)} \ \ \ \ \ (43)$

No triângulo rectângulo ${DEF}$ , recto em ${E}$ , o ângulo sobre o vértice ${D}$ é ${r}$ , logo: ${cos (r)= \frac{DE}{DF}=\frac{e}{DF}}$ . Então:

$\displaystyle DF=\frac{e}{cos (r)} \ \ \ \ \ (44)$

Combinando as expressões 43 com 44, obtemos :

$\displaystyle d=\frac{e . sen (i-r)}{cos (r)} \ \ \ \ \ (45)$

O afastamento entre os raios será directamente proporcional a espessura da lâmina. Podemos também verificar, experimentalmente , que o afastamento entre os raios ${d}$ aumenta com o aumento do ângulo de incidência. Mas demonstrar isso matematicamente acaba por ser um pouco extenso. Por outro lado, se consideramos o triângulo ${CHI}$ , recto em ${I}$ , o ângulo sob o vértice ${C}$ será ${90^0-i}$ . Logo, o seu cosseno será ${cos ( 90^0-i)=\frac{CI}{CH}=\frac{d}{\delta}}$ . Lembre-se que ${cos(90^0-i)=sen (i) \Rightarrow sen (i)=\frac{d}{\delta}\Rightarrow d= \delta . sen (i)}$ . Substituindo isso na equação 43, obtemos:

$\displaystyle \delta=\frac{e . sen (i-r)}{cos (r). sen (i)}\ \ \ \ \ (46)$

Desenvolvendo o seno da diferença, separando os denominadores, e simplificando, obtemos a expressão obtemos:

$\displaystyle \delta=(1-\frac{cos(i)}{n . cos (r)}).e \ \ \ \ \ (47)$

Quando a lâmina é bastante delgada (fina, pouco espessa), podemos considerar que o raio emergente é confundido com o raio incidente.

Está a gostar da Abordagem? Veja também:

— Referências Bibliográficas —

Equações diferenciais de Bernoulli e Ricatti. Redução a separação de variáveis

02/10/2016 11:03 pm / 3 comentários em Equações diferenciais de Bernoulli e Ricatti. Redução a separação de variáveis

— 2.5. Equação de Bernoulli —

Neste artigo, não estudaremos nenhum tipo particular para equação diferencial.Consideraremos duas equações clássicas que podem ser transformadas em equações já estudadas nas seções anteriores e depois vamos abordar sobre redução a separação de variáveis.

Definição 14.A equação diferencial

$\displaystyle \dfrac{dy}{dx}+P(x)y=Q(x)y^{n} \ \ \ \ \ (11)$

em que n é um numero real qualquer, é chamada de equação de Bernoulli.Para ${n=0}$ e ${n=1}$ a equação (11) é linear em y.Agora se ${y\neq0}$ ,a equação (11) pode ser escrita da seguinte maneira:

$\displaystyle y^{-n}\dfrac{dy}{dx}+P(x)y^{1-n}=Q(x) \ \ \ \ \ (12)$

se fizermos ${w=y^{1-n},\quad n\neq0,\quad n\neq1,}$ então:

$\displaystyle \dfrac{dw}{dx}=(1-n)y^{-n}\dfrac{dy}{dx}$

com essa substituição, a equação (12) transforma-se na equação linear

$\displaystyle \dfrac{dw}{dx}+(1-n)P(x)w=(1-n)Q(x) \ \ \ \ \ (13)$

Resolvendo a equação (13) e depois fazendo ${y^{1-n}=w}$ , obtemos uma solução para a equação (11).

Exemplo 1.Resolva a seguinte equação

$\displaystyle \dfrac{dy}{dx}+\dfrac{1}{x}y=xy^{2}$

Solução:De acordo a equação de Bernoulli temos: ${P(x)=1/x,\quad Q(x)=x, \quad e \quad n=2}$ .logo, a mudança de variável

$\displaystyle w=y^{-1}\Rightarrow \dfrac{dw}{dx}=-y^{-2}\dfrac{dy}{dx}\Rightarrow \dfrac{dy}{dx}=-y^{2}\dfrac{dw}{dx}$

nos da o seguinte:

$\displaystyle -y^{2}\dfrac{dw}{dx}+\dfrac{1}{x}y=xy^{2}\Rightarrow \dfrac{dw}{dx}-\dfrac{1}{x}y^{-1}=-x$

substituindo ${w=y^{-1}}$ teremos:

$\displaystyle \dfrac{dw}{dx}-\dfrac{1}{x}w=-x$

o fator de integração para essa equação linear é:

$\displaystyle \mu(x)=e^{-\int \frac{dx}{x}}=e^{-ln x}=x^{-1}$

assim,multiplicando o fator de integração na equação linear, teremos:

$\displaystyle x^{-1}\dfrac{dw}{dx}-x^{-2}w=-1\Rightarrow \dfrac{d}{dx}(x^{-1}w)=-1$

integrando essa ultima forma, obtemos

$\displaystyle x^{-1}w=-x+c \quad ou \quad w=-x^{2}+cx$

como ${w=y^{-1}}$ , então ${y=\frac{1}{w}}$ ou

$\displaystyle y=\dfrac{1}{-x^{2}+cx}$

— 2.6. Equação de Ricatti —

Definição 15.A equação diferencial linear

$\displaystyle \dfrac{dy}{dx}=P(x)+Q(x)y+R(x)y^{2} \ \ \ \ \ (14)$

é chamada de equação de Ricatti.Se ${y_{1}}$ é uma solução particular para (14),então as substituições

$\displaystyle y=y_{1}+u \quad e \quad \dfrac{dy}{dx}=\dfrac{dy_{1}}{dx}+\dfrac{du}{dx}$

em (14) produzem a seguinte equação diferencial para u:

$\displaystyle \dfrac{du}{dx}-(Q+2y_{1}R)u=Ru^{2} \ \ \ \ \ (15)$

como (15) é uma equação de Bernoulli com ${n=2}$ , ela pode, por sua vez, ser reduzida a equação linear

$\displaystyle \dfrac{du}{dx}+(Q+2y_{1}R)u=-R \ \ \ \ \ (16)$

através da substituição ${w=u^{-1}}$ .Depois de fazer essa substituição podemos aplicar os outros métodos estudados.

Exemplo 2.Considere a equação

$\displaystyle \dfrac{dy}{dx}=e^{2x}+(1+2e^{x})y+y^{2}$

Verifica-se que ${y_{1}=-e^{x}}$ é uma solução particular desta equação.Fazendo a substituição

$\displaystyle y=-e^{x}+u\Rightarrow \dfrac{dy}{dx}=-e^{x}+\dfrac{du}{dx}$

teremos:

$\displaystyle -e^{x}+\dfrac{du}{dx}=e^{2x}+(1+2e^{x})(-e^{x}+u)+(-e^{x}+u)^{2}$

simplificando a equação obtemos a seguinte expressão

$\displaystyle \dfrac{du}{dx}=u+u^{2}$

a equação acima é uma equação de Bernouli, então,vamos fazer a seguinte substituição:

$\displaystyle w=u^{-1}\Rightarrow \dfrac{dw}{dx}=-y^{-2}\dfrac{du}{dx}\Rightarrow \dfrac{du}{dx}=-u^{2}\dfrac{dw}{dx}$

logo, teremos:

$\displaystyle -u^{2}\dfrac{dw}{dx}=u+u^{2}\Rightarrow \dfrac{dw}{dx}=-\dfrac{1}{u}-1\Rightarrow \dfrac{dw}{dx}=-w-1$

a ultima equação é de variáveis separáveis de modo que resolvendo teremos:

$\displaystyle ln (w+1)=-x+c_{1}\Rightarrow w=e^{-x+c_{1}}-1\Rightarrow w=ce^{-x}-1$

substituindo ${w=u^{-1}}$ temos:

$\displaystyle u^{-1}=ce^{-x}-1\Rightarrow u=\dfrac{1}{ce^{-x}-1}$

substituindo ${u=y+e^{x}}$ obtemos que a solução da equação é dada por:

$\displaystyle y=\dfrac{1}{ce^{-x}-1}-e^{x}$

— 2.7. Redução a Separação De Variáveis —

Definição 16.Uma equação diferencial da forma

$\displaystyle \dfrac{dy}{dx}=f(Ax+By+c)$

se pode sempre reduzir a uma equação com variáveis separáveis por meio da substituição ${u=Ax+By+c}$ , ${B\neq0}$

Exemplo 3.Resolva a seguinte equação diferencial

$\displaystyle \dfrac{dy}{dx}=(-2x+y)^{2}-7, \quad y(0)=0$

Solução:Vamos resolve-la fazendo a substituição

$\displaystyle u=-2x+y\Rightarrow \dfrac{du}{dx}=-2+\dfrac{dy}{dx}$

dessa maneira a equação diferencial se expressa da seguinte forma:

$\displaystyle \dfrac{du}{dx}+2=u^{2}-7\Rightarrow \dfrac{du}{dx}=u^{2}-9$

essa ultima equação é de variáveis separáveis de modo que teremos:

$\displaystyle \dfrac{du}{(u-3)(u+3)}=dx\Rightarrow \dfrac{1}{6}\left[\dfrac{1}{u-3}-\dfrac{1}{u+3}\right]du=dx$

e depois de integrar vamos ter:

$\displaystyle \dfrac{1}{6}ln \left[\dfrac{u-3}{u+3}\right]=x+c_{1}\Rightarrow \dfrac{u-3}{u+3}=e^{6x+6c_{1}}$

substituindo ${e^{6c_{1}}}$ por c e isolando u obtemos o seguinte:

$\displaystyle u=\dfrac{3(1+ce^{6x})}{1-ce^{6x}}$

substituindo ${u=-2x+y}$ na equação acima obtemos a seguinte solução:

$\displaystyle y=2x+\dfrac{3(1+ce^{6x})}{1-ce^{6x}}$

por ultimo aplicando a condição inicial ${y(0)=0}$ a ultima equação obtém-se ${c=-1}$ de modo que a solução particular será:

$\displaystyle y=2x+\dfrac{3(1-e^{6x})}{1+e^{6x}}$

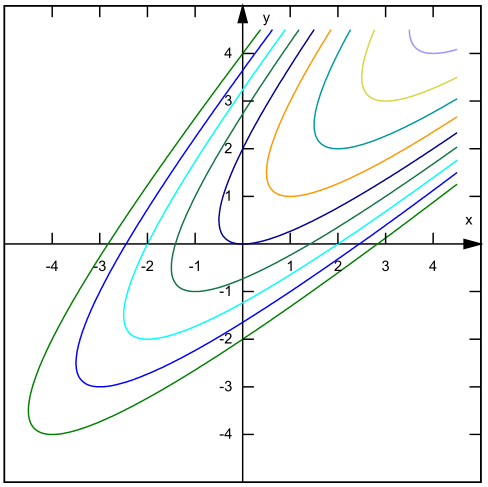
a figura abaixo mostra em azul escuro o gráfico da solução particular junto com o gráfico de outros membros da família de soluções.

eqdf3

Figura 1:Algumas soluções do Exemplo 3

Nas seções precedentes, vimos que em certas situações uma equação diferencial podia ser ser transformada, por meio de uma substituição, em uma forma em que era possível resolve-la por um método padrão.Uma equação pode parecer diferente de todas as que vimos e estudamos, mas mudando uma variável, talvez um problema aparentemente difícil possa ser facilmente resolvido.Embora não haja uma regra geral que indique qual substituição deve ser feita,uma axioma pratico é o seguinte:tente alguma coisa!Algumas vezes custa caro ser engenhoso.

Exemplo 4.Considere a equação

$\displaystyle \dfrac{dy}{dx}=\dfrac{y-x}{y-x-1}$

se olharmos bem a equação, podemos ser impelidos a tentar a substituição

$\displaystyle u=y-x\Rightarrow \dfrac{du}{dx}=\dfrac{dy}{dx}-1\Rightarrow \dfrac{dy}{dx}=\dfrac{du}{dx}+1$

substituindo na equação temos:

$\displaystyle \dfrac{du}{dx}+1=\dfrac{u}{u-1}\Rightarrow \dfrac{du}{dx}=\dfrac{1}{u-1}\Rightarrow (u-1)\dfrac{du}{dx}=1$

que é uma equação de variável separável cuja solução é:

$\displaystyle \dfrac{u^{2}}{2}-u=x+c$

Substituindo-se de volta ${u=y-x}$ obtemos que a solução da equação é dada implicitamente por

$\displaystyle \dfrac{(y-x)^{2}}{2}-y=c$

eqdf4

Figura 2:soluções da equação do Exemplo 4

Luso Academia

Monthly Archives: Fevereiro 2016

Aplicação das equações diferenciais de primeira ordem.Misturas

Porquê o peixe parece maior? Refração em superfície esférica.

Aplicação das equações diferenciais de primeira ordem.Corpos em queda

Aplicação das equações diferenciais de primeira ordem.Circuitos elétricos

Conheça a física dos óculos. Lentes. Características principais.

Luso Academia no Facebook

Aplicações das equações diferenciais de primeira ordem.

Como a Física explica o arco-íris? Dispersão da luz. Prisma.

Está a gostar da Abordagem? Veja também:

Exercícios e Problemas resolvidos e explicados de Mecânica (Física 1);

Exercícios e Problemas resolvidos e explicados de Termodinâmica (Física 2);

Exercícios e Problemas resolvidos e explicados de Gravitação (Física 2);

Exercícios e Problemas resolvidos e explicados de Oscilações e Ondas (Física 2);

Exercícios e Problemas resolvidos e explicados de Fluidos (Física 2);

Exercícios e Problemas resolvidos e explicados de Electromagnetismo (Física 3);

Exercícios e Problemas resolvidos e explicados de Luz e Óptica (Física 4);

Exercícios e Problemas resolvidos e explicados de Física Moderna e Mecânica Quantia (Física 4);

Exercícios e Problemas resolvidos e explicados de Equações diferenciais ordinárias;

Exercícios e Problemas resolvidos e explicados de Cálculo;

Todas as Categorias (Início).

Como a Física explica a deformação da imagem dos corpos submersos na água?

Está a gostar da Abordagem? Veja também:

Exercícios e Problemas resolvidos e explicados de Mecânica (Física 1);

Exercícios e Problemas resolvidos e explicados de Termodinâmica (Física 2);

Exercícios e Problemas resolvidos e explicados de Gravitação (Física 2);

Exercícios e Problemas resolvidos e explicados de Oscilações e Ondas (Física 2);

Exercícios e Problemas resolvidos e explicados de Fluidos (Física 2);

Exercícios e Problemas resolvidos e explicados de Electromagnetismo (Física 3);

Exercícios e Problemas resolvidos e explicados de Luz e Óptica (Física 4);

Exercícios e Problemas resolvidos e explicados de Física Moderna e Mecânica Quantia (Física 4);

Exercícios e Problemas resolvidos e explicados de Equações diferenciais ordinárias;

Exercícios e Problemas resolvidos e explicados de Cálculo;

Todas as Categorias (Início).

Equações diferenciais de Bernoulli e Ricatti. Redução a separação de variáveis

Navegação de artigos

Monthly Archives: Fevereiro 2016

Partilhar

Partilhar

Partilhar

Partilhar

Partilhar

Partilhar

Partilhar

Está a gostar da Abordagem? Veja também:

Partilhar

Está a gostar da Abordagem? Veja também:

Partilhar

Partilhar

Navegação de artigos