Início » 03 Ensino Médio » 01 Matemática

Category Archives: 01 Matemática

Continuidade em Espaços Métricos. Continuação.

09/22/2019 10:03 pm / Deixe um comentário

— 1.2.10. Continuidade em Espaços Métricos. Continuação —

Agora apresentaremos alguns exemplos de funções contínuas. Vou assumir que os leitores já estão familiarizados com a noção de continuidade apresentada nos cursos de Cálculo, principalmente as funções trigonométricas, logaritimicas e polinomiais. Em seguida, darei alguns exemplos sobre o conceito de continuidade nos espaços métricos.

Proposição 33 Seja ${(X,d)}$ um espaço métrico e ${A\subseteq X}$ , com ${A\neq\emptyset}$ . Então para todo ${x,y\in X}$ e ${z\in A}$ , temos:

$\displaystyle \mid d(x,A)-d(y,A)\mid\leq d(x,y) \ \ \ \ \ (2)$

Demonstração: Como ${X}$ éum espaço métrico, então é válida a desigualdade triângular:

$\displaystyle d(x,y)\leq d(x,z)+d(z,y)$

tomando o ínfimo para todo ${z\in A}$ e considerando

$\displaystyle d(x,A)=\inf_{z\in A}d(x,z)$

$\displaystyle d(y,A)=\inf_{z\in A}d(y,z)$

teremos, ${d(x,A)-d(y,A)\leq d(x,y)}$ , e depois trocando ${x}$ e ${y}$ se obtem:

$\displaystyle \mid d(x,A)-d(y,A)\mid\leq d(x,y)$

$\Box$

Proposição 34 Seja ${(X,d)}$ um espaço métrico, e ${x_{0}\in X}$ . Se definirmos a função distância ${f:X\longrightarrow \mathbb{R}}$ , como

$\displaystyle f(x)=d(x,x_{0})$

então ${f}$ é contínua.

Demonstração: Para provarmos isto usaremos a Prop. 1.31 assim como a 1.33. Sabemos que uma função é contínua em um ponto ${a}$ se e só se ${\forall x_{n}\subset X: x_{n}\longrightarrow a\implies f(x_{n})\longrightarrow f(a)}$ .

É importante notarmos que na definição da função distância o espaço imagem é basicamente ${(Y=\mathbb{R},\rho_{\text{usual}})}$ portanto, ${\rho(f(x),f(y))=\mid f(x)-f(y)\mid}$ .

Seja ${x_{n}}$ uma sequência de ${X}$ tal que : ${x_{n}\longrightarrow a}$ , então por definição ${d(x_{n},a)<\epsilon}$ , onde ${\epsilon>0}$ . Logo,

$\displaystyle \rho(f(x_{n}),f(a))=\mid f(x_{n})-f(a)\mid=\mid d(x_{n},x_{0})-d(x_{0},a)\mid\leq d(x_{n},a)<\epsilon$

Portanto, é suficiente tomar ${\delta=\delta(a,\epsilon)=\epsilon}$ e ${d(x,a)<\delta}$ , para garantirmos a continuidade de ${f}$ . E como ${a\in X}$ é arbitrário isto significa que ${f(x)=d(x,x_{0})}$ é contínua para todo ${\mathbb{R}}$ . $\Box$

Exemplo 13

Se ${(X,d)}$ é um espaço métrico discreto e ${(Y,\rho)}$ um espaço métrico qualquer, então as únicas funções contínuas ${f:x\longrightarrow Y}$ são as funções constantes.
Para provarmos isto, seja ${\epsilon>0}$ basta tomar ${\delta<1}$ , com ${d(x,a)<\delta<1}$ e como ${d}$ é a métrica discreta, i.e.,

$\displaystyle d(x,y) = \left \{ \begin{array}{cl} 1 & \mbox{, } x\neq y\\ 0 & \mbox{, } x= y \end{array}\right.$

então obviamente ${d(x,a)=0}$ o que implica ${x=a}$ . Assim,

$\displaystyle \rho(f(x),f(a))=\rho(f(a),f(a))=0.$
A função ${f:\mathbb{R}\times\mathbb{R}^{n}\longrightarrow\mathbb{R}^{n}}$ definida como:
$\displaystyle f(k,x)=kx$

é contínua.(É facíl provar, deixada ao leitor, não esquecer que ${x\in\mathbb{R}^{n}}$ é um vector, i.e., ${x=(x_{1},\cdots,x_{n})}$ ).

Proposição 35 Seja ${(X,d)}$ um espaço métrico e ${f,g:X\longrightarrow \mathbb{R}}$ duas funções contínuas. Então:

${(f+g)(x)=f(x)+g(x)}$ e ${(fg)(x)=f(x)g(x)}$ são contínuas.
Se ${f(x)\neq0}$ para todo ${x\in X}$ , então ${h(x)=\frac{1}{f(x)}}$ é uma função contínua.

Demonstração: Deixada ao leitor. $\Box$

O conceito de continuidade reveste-se de capital importância para a Topologia por isso em aulas subsequentes continuaremos a explorar o conceito até as suas aplicações mais importantes.

Função composta

08/25/2015 6:41 pm / Deixe um comentário

— 1. Conceito —

Definição 1 Dados três conjuntos ${ A }$ , ${ B }$ e ${ C }$ não vazios. seja ${ f }$ uma função de ${ A }$ em ${ B }$ e ${ g }$ outra função de ${ B }$ em ${ C }$ . Chama-se função composta de ${ f }$ e ${ g }$ a função ${ h }$ de ${ A }$ em ${ C }$ definida por:

$\displaystyle h(x)=f(g(x)) \ \ \ \ \ (1)$

se ${\forall x\in A }$

Muita das vezes representa-se por ${ h(x)=fog \ \forall x\in A }$ e lê-se: ${ f }$ composta por ${ g }$ ,

então ${ (fog)(x)=f(g(x)) \ \forall x\in A }$

por diagrama temos:

A mesma ideia podemos representar também dessa maneira:

Exercício 1

Dados os conjuntos ${ A=(1,2,3) }$ , ${ B=(-1,2,5,7) }$ e ${ C=(-1,5,11,15) }$ .

Seja a função ${ f(x)=x^2-2 }$ de ${ A }$ em ${ B }$ e a outra ${ g(x)=2x+1 }$ de ${ B }$ em ${ C }$ , calcular ${ h=gof }$

Resolução

${ f:A\rightarrow B }$ .

Para ${ x=1 }$ temos: ${ f(x)=x^2-2 \rightarrow f(1)=(1)^2-2=1-2=-1 \leftrightarrow f(1)=-1 }$

Para ${ x=2 }$ temos: ${ f(x)=x^2-2 \rightarrow f(2)=(2)^2-2=4-2=2 \leftrightarrow f(2)=2 }$

Para ${ x=1 }$ temos: ${ f(x)=x^2-2 \rightarrow f(3)=(3)^2-2=9-2=7 \leftrightarrow f(3)=7 }$

${ g:B\rightarrow C }$ , temos:

Para ${ x=-1 }$ temos: ${ g(x)=2x+1 \rightarrow g(-1)=2(-1)+1=-2+1=-1 \leftrightarrow g(-1)=-1 }$

Para ${ x=2 }$ temos: ${ g(x)=2x+1 \rightarrow g(2)=2(2)+1=4+1=5 \leftrightarrow g(2)=5 }$

Para ${ x=5 }$ temos: ${ g(x)=2x+1 \rightarrow g(5)=2(5)+1=10+1=11 \leftrightarrow g(5)=11 }$

Para ${ x=7 }$ temos: ${ g(x)=2x+1 \rightarrow g(7)=2(7)+1=14+1=15 \leftrightarrow g(7)=15 }$

Agora podemos calcular a função composta definida por ${ h(x)=gof=g(f(x)) \forall x \in A }$

Para ${ x=1 }$ temos: ${ h(x)=g(f(x)) \leftrightarrow h(1)=g(f(1))=g(-1)=-1 \leftrightarrow h(-1)=-1 }$

Para ${ x=2 }$ temos: ${ h(x)=g(f(x)) \leftrightarrow h(2)=g(f(2))=g(2)=5 \leftrightarrow h(2)=5 }$

Para ${ x=3 }$ temos: ${ h(x)=g(f(x)) \leftrightarrow h(3)=g(f(3))=g(7)=15 \leftrightarrow h(3)=15 }$

por diagrama, temos:

Observando muito bem ${ h(x)=gof \forall x \in A }$ o conjunto ${ Im \subset C }$ , então temos:

${ h(x)=gof }$ de ${ A }$ em ${ C }$

Exercício 2

Dadas as funções reais ${ g(x)=x^2+4 }$ e ${ f(x)=x-3 }$ , determinar a função composta ${ h(x)=g(f(x)) }$

Resolução

Temos:

${ h(x)=g(f(x))=g(x-3)=(x-3)^2+4=x^2-6x+9+4=x^2-6x+13 }$

${ \leftrightarrow h(x)=g(f(x))=x^2-6x+13 }$

Teorema 1

${ g }$ composta com ${ f }$ em geral não é igual a ${ f }$ composta com ${ g }$

$\displaystyle gof \neq fog \ \ \ \ \ (2)$

Demonstração:

Sejam ${ x \in A }$ , ${ y \in B }$ e ${ u \in B }$ e ${ v \in D }$ . Suponhamos que ${ y=f(x) }$ de ${ A }$ em ${ B }$ , ${ u=g(y) }$ de ${ B }$ em ${ C }$ e ${ v=h(u) }$ de ${ C }$ em ${ D }$ ;

temos:

${ (gof)(x)=g(f(x))=g(y)=u \leftrightarrow gof=u }$

${ (fog)(y)=f(g(y))=f(u) \leftrightarrow fog=f(u) }$ contradição porque

${ u \in C }$ e ${ f: A \rightarrow B }$

logo: ${ gof \neq fog }$

$\Box$

Exercício 3

Sejam as funções ${ f(x)=-2x+3 }$ e ${ g(x)=x-x^2 }$ , Calcular ${ gof }$ e ${ fog }$

Resolução: Temos:

${ gof=g(f(x))=-2(x-x^2)+3=-2x+2x^2+3=x^2-2x+3 }$

${ \leftrightarrow gof=x^2-2x+3 }$

${ fog=f(g(x))=(-2x+3)-(-2x+3)^2=(-2x+3)-(4x^2-6x+9)}$

${ \leftrightarrow f(f(x))=-2x+3-4x^2+6x-9=-4x^2+4x-6 }$

${ \leftrightarrow fog=-4x^2+4x-6 }$

Verificando o teorema

${ gof\neq fog }$

Exercício 4

Sejam as funções ${ f(x)=x^2-5x+6 }$ e ${ g(x)=x^2 }$ , Calcular: ${ (gof)(1) }$ e ${ (fog)(1) }$

Temos:

${ gof=g(f(x))=(x^2-5x+6)^2=x^4-10x^3+37x^2-60x+36 }$

calculando ${ (gof)(1) }$ ,

temos:

${ (gof)(1)=g(f(1))=1^4-10(1)^3+37(1)^2-60(1)+36=4 \leftrightarrow (gof)(1)=4 }$

${ (fog)=f(g(x))=(x^2)^2-5x^2+6=x^4-5x^2+6 \leftrightarrow fog=x^4-5x^2+6 }$

Calculando ${ (fog)(1)}$ , temos:

${ (fog)(1)=f(g(1))=(1)^4-5(1)^2+6=2 ,\leftrightarrow (gof)(1)=4 }$

Verificando o teorema, vemos que ${ gof \neq fog }$

Exercício 5

Sejam as funções ${ f: \mathbb{R} \rightarrow \mathbb{R} }$ e ${ g: \mathbb{N} \rightarrow \mathbb{R} }$ definidas por ${ f(x)=x+2 }$ e ${ g(x)=\dfrac{2}{x^2} }$ , determinar ${ f(g(x)) }$ e ${ g(f(x)) }$

Resolução:

Temos:

${ f(g(x))=\dfrac{2}{x^2}+2=\dfrac{2+2x^2}{x^2} \leftrightarrow f(g(x))= \dfrac{2+2x^2}{x^2} }$

${\leftrightarrow f(g(x)): \mathbb{N} \rightarrow \mathbb{R} }$

isto é verdade; logo ${ f(g(x))=\dfrac{2+2x^2}{x^2} }$ de ${ \mathbb{N} }$ em ${ \mathbb{R} }$

${ g(f(x))= \dfrac{2}{(x+2)^2} \leftrightarrow g(f(x)):\mathbb{R} \rightarrow \mathbb{R} }$ que não é verdade

como ${ x\in R }$ , tomemos ${ x=-2 }$ a função ${ g(f(x))= \dfrac{2}{(x+2)^2} }$ não está definida; logo não é uma função de ${ R }$ em ${ R }$

Teorema 2

A função composta é associativa.

$\displaystyle (hog)of=ho(fog) \ \ \ \ \ (3)$

Demonstração:

Sejam os elementos ${ x\in A }$ , ${ y\in B }$ , ${ u\in C }$ e ${ v\in D }$ . Suponhamos que ${ y=f(x) }$ de ${ A }$ em ${ B }$ , ${ u=g(y) }$ de ${ B }$ em ${ C }$ e

${ v=h(u) }$ de ${ C }$ em ${ D }$ ;

temos:

${ (hog)of=(hog)of)x=(hog)f(x)=(hog)y=h(g(y))=h(u)=v }$

${\leftrightarrow (hog)of=v }$

${ ho(gof)(x)=ho(g(f(x)))=ho(g(y))=h(u)=v \leftrightarrow ho(gof)=v }$

Assim mostramos que: ${ (hog)of=ho(fog) }$

$\Box$

Exercício 6

Dadas as funções ${ f(x)=3-x }$ e ${ g(x)=(x+1)^2 }$ e ${ h(x)=3x }$ ,

Calcular ${ (hog)of }$ e ${ ho(fog)}$ e verifique o teorema.

temos:

${ (hog)of=(h(g(x))of=3(x+1)^2=3f(x)^2+6f(x)+3=3(3-x)^2+6(3-x)+3 }$

${ \Longrightarrow (hog)of=3x^2-24x+48 }$

${ ho(gof)=ho(g(f(x)))=h(-x+4)^2)=3(-x+4)^2=3x^2-24x+48 }$

Claramente que são iguais

Teorema 3

Se ${ f }$ e ${ g }$ são sobrejectivas então a função composta

$\displaystyle fog \ \ \ \ \ (4)$

também é sobrejectira

Demonstração:

Sejam os elementos ${ x\in A }$ , ${ y\in B }$ , ${ u\in C }$ e ${ v\in D }$ . Suponhamos que ${ y=f(x) }$ de ${ A }$ em ${ B }$ , ${ u=g(y) }$ de ${ B }$ em ${ C }$ e

${ v=h(u) }$ de ${ C }$ em ${ D }$ ;

temos:

Como ${ g }$ é sobrejectiva, então

${ \forall u\in C }$ , ${ \exists y\in B }$ de modo que ${ g(y)=u }$

a função ${ g }$ é sobrejectiva, então

${ \forall y\in B }$ , ${ \exists x\in A }$ de modo que ${ f(x)=y }$ então,

${ \forall u\in C, \exists x\in A: u=g(y)=g(f(x))=(gof)(x) }$

Assim provamos que ${ gof }$ sobrejectiva.

$\Box$

Teorema 4

Se duas funções ${ f }$ e ${ g }$ são injectivas, então a função composta

$\displaystyle fog \ \ \ \ \ (5)$

também é injectiva

Demonstração:

Seja ${ \forall x_{1} \in A }$ e ${ \forall x_{2} A }$ . Suponhamos ${ (gof)(x_{1})=(gof)(x_{2}) }$ logo, ${ g(f(x_{1})=g(f(x_{2}) }$ . Como ${ g }$ é injectiva, então

${ g(f(x_{1})=g(f(x_{2}) }$ , como ${ f }$ também é, então ${ x_{1}=x_{2} }$ implica que ${ gof }$ é injectiva.

$\Box$

Teorema 5

Sejam as função ${ f: A\rightarrow B }$ e ${ f^{-1}: B \rightarrow A }$ ,então

$\displaystyle f^{-1}of= \vert_{A} \ e \ fof^{-1}= \vert_{B} \ \ \ \ \ (6)$

onde: ${ \vert_{A} \ e \ \vert_{B} }$ são funções identidade.

Demonstração:

Sejam os elementos ${ x \in A }$ , ${ y \in B }$ e ${ u \in C }$ . Suponhamos que ${ y=f(x) }$ de ${ A }$ em ${ B }$ e a inversa ${ x=f(y) }$ de ${ B }$ em ${ A }$ ,temos:

${ \forall x \in A (f^{-1}of)(x)=f^{-1}(f(x))=f^{1}(y)=x \leftrightarrow (f^{-1}of)(x)=x }$ , é verdade que ${ x \in A }$

${\forall y \in B (fof^{-1})(y)=f(f^{-1}(y))=f(x)=y \leftrightarrow (fof^{-1})(y)=y }$ é verdade que ${ y \in B }$

$\Box$

Teorema 6

Se a função ${ f:A \rightarrow B }$ e ${ g:B \rightarrow C }$ são bijectivas então:

$\displaystyle (gof)^{-1}=f^{-1}og^{-1} \ \ \ \ \ (7)$

Demonstração:

Sejam ${ x\in A }$ , ${ y \in B }$ e ${ u \in C }$ . Suponhamos que ${ y=f(x) }$ de ${ A }$ em ${ B }$ e a inversa ${ u=g(y) }$ de ${ B }$ em ${ A }$ .

Vamos supor também que ${ f }$ e ${ g }$ são mesmo bijectivas, logo ${ gof }$ de ${ A }$ em ${ C }$ também é bijectiva ,então ${ (gof)^{-1} }$ de ${ C }$ em ${ A }$

Sendo assim; demonstrar que ${(gof)^{-1}=f^{-1}og^{-1} }$ equivale mostrar que ${ (f^{-1}og^{-1})o(gof)=\vert_{A} }$ e ${(gof)o(f^{-1}og^{-1}=\vert_{C} }$

Temos:

${ (f^{-1}og^{-1})o(gof)=((f^{-1}og^{-1})og)of=(f^{-1}(g^{-1}og))of=(f^{-1}o\vert_{B})of=f^{-1}of=\vert_{A} }$

${ (gof)(f^{-1}og^{-1})=((gof)of^{-1})og^{-1}=( g(fof^{-1}))og^{-1}=(go\vert_{A})og^{-1}=gog^{-1}=\vert_{c}}$

Assim demonstramos que ${(gof)^{-1}=f^{-1}og^{-1} }$ se ${ f }$ e ${ g }$ forem bijectivas.

$\Box$

— 2. Exercícios complementares —

Exercício 7 Sejam as funções ${ g(x)=2x+3 }$ e

${ \left.f(x)=\lbrace \begin{array}{ll} x^2-2x & se \ x \geq 2;\\ x^2 & se \ x < 2 \end{array} \right. }$ determinar ${ f(g(x) }$

Resolução Temos: fazer ${ y=g(x) }$ ${ 1 }$ ) Para ${ x\geq 2 \leftrightarrow 2x+3 \geq 2 \leftrightarrow x \geq - \dfrac{1}{2} }$

${ f(g(x))= (2x+3)^2-2(2x+3)=4x^2+12x+9-4x-6=4x^2+8x+3 }$

${ 2 }$ ) para ${ x<2 \rightarrow 2x+3<2 \leftrightarrow x<-\dfrac{1}{2} }$

${ f(g(x))=-3(2x+3)+2=-6x-9+=-6x-7 }$

então,

${ \left.f(g(x))=\lbrace \begin{array}{ll} x^2+8x+3 & se \ x\geq -\dfrac{1}{2};\\ -6x-7 & se \ x < -\dfrac{1}{2} \end{array} \right. }$

Exercício 8

Dadas as funções ${ g(x)=\sqrt{x} }$ e ${ s(x)=\sqrt{1-x^2} }$ ,

determinar ${ gos }$ e ${ sog }$

Resolução Temos:

${ gos=g(s(x))=\sqrt{\sqrt{1-x^2}}=\sqrt[4]{1-x^2} }$

${ sog=s(g(x))=\sqrt{1-\sqrt{x^2}}=\sqrt{1-x} }$

Exercício 9

Dadas as funções ${ f(g(x))=4x+11 }$ e ${ g(x)=x+2 }$ determinar ${ f(g(x) }$

Resolução Temos:

${ f(g(x))=4x+11 \leftrightarrow f(x+2)=4x+11}$

fazendo ${ t=x+2 \leftrightarrow x=t-2 }$ ,

tem-se: ${ f(t)=4(t-2)+11=4t-8+11=4t+3 \rightarrow f(x)=4x+3}$

Exercício 10 Dadas as funções ${ g(f(x))=4x^2-12x+10 }$ e ${ f(x)=2x-3 }$ determinar ${ g(-4) }$

Resolução Temos:

${ g(f(x))=4x^2-12x+10 \leftrightarrow f(2x-3)=4x^2-12x+10 }$

fazendo ${ t=2x-3 \leftrightarrow x=\dfrac{t+3}{2} }$ ,

tem-se:

${ g(t)=4(\dfrac{t+3}{2})^2-12(\dfrac{t+3}{2})+10 }$

${\leftrightarrow g(t)=4(\dfrac{t^2+6t+9}{4})-6(t+3)+10=t^2+6t+9-6t-18+10 }$

${ \leftrightarrow g(t)=t^2+1 \rightarrow g(x)=x^2+1}$

Calculando ${ g(-4) }$ ,

temos:

${ g(-4)=(-4)^2+1=16+1=17 }$

Exercício 11 Dadas as funções ${ g(x)=ax+b }$ e ${ f(x)=cx^2+d }$ .

a) Qual é a condição que satisfaz a igualdade ${ f(g(x))=g(f(x))}$ ?

b) Mostre que ${ (fog)(0))-g(f(0))=d(a-1)+b(c-b) }$

Resolução Temos:

a) ${ f(g(x))=a(cx^2+d)+b=acx^2+ad+b }$

${ g(f(x))=c(ax+b)^2+d=c(a^2x^2+2abx+b^2)+d=ca^2x^2+2cabx+cb^2+d }$

para que ${ f(g(x))=g(f(x)) }$ , temos:

${ acx^2+ad+b=ca^2x^2+2cabx+cb^2+d }$

Utilizando identidade de polinómios, temos:

${ abc=0 }$ e ${cb^2+d=b }$

Resolvendo o sistema resulta: ${ f(g(x))=g(f(x)) }$

${ \left.f(g(x))=g(f(x)) \leftrightarrow \lbrace \begin{array}{ll} cd^2+d=b & se \ a=0 ;\\ d=b & se \ c=0 \end{array} \right. }$

b) ${(fog)(0))-g(f(0))=(ac(0)^2+ad+b)-(ca^2(0)^2+2cab(0)+cb^2+d)}$ ${ \leftrightarrow (fog)(0)=ad+b -cb^2-d=d(a-1)+b(c-b) }$

Exercício 12

Dadas as funções ${ f(x)=2x+y }$ e ${ g(x)=\dfrac{1}{4} }$ ,

determinar o produto de ${ fof }$ com ${ gog }$ sabendo que ${ a \in N }$ e ${ y \in N }$ e ${ a \neq y }$ .

Resolução: Vamos resolver ${ f(f(x)) }$ , isto é, composta de ${ f }$ por si mesmo, assim temos: ${ f(f(x))=2(2x+y)+y=2x+3y }$ e ${ g(g(x))=\dfrac{a}{4} }$

O produto é ${(2x+3y)(\dfrac{a}{4})=\dfrac{2ax+3ay}{4}}$

como ${ a }$ e ${ y }$ são números naturais e pares e diferentes, então temos:

fazendo ${ a=2k }$ e ${ y=4k \forall k\in\mathbb{N}}$ resulta:

${\dfrac{2ax+3ay}{4}=\dfrac{4kx+24k^2}{4}=kx+6k^2}$ .

Domínio contradomínio e imagem de função.

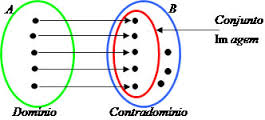
08/20/2015 6:25 pm / 11 comentários em Domínio contradomínio e imagem de função.

— 1. Introdução —

Não existe uma função ${ f }$ sem domínio, sem contradomínio e sem imagem. Os três elementos citados são inseparáveis a função.

Sendo assim, vamos, então começar a definir os três elementos fundamentais da função. Seja a função ${ f }$ : ${ A \rightarrow B }$ . Por diagrama, temos:

Definição 1 -Chama-se domínio da função ${ f }$ , o conjunto D de todos elementos ${ x }$ do conjunto A. Matematicamente, temos:

$\displaystyle D(f)=\lbrace x\in\mathbb{R}\vert \forall x\in A\rbrace \rightarrow D(f)=A \ \ \ \ \ (1)$

Definição 2 – Chama-se contradomínio da função ${ f }$ , o conjunto ${ CD }$ de todos elementos de ${ B }$ . Matematicamente, temos:

$\displaystyle CD(f)=\lbrace y \in \mathbb{R} \vert \forall y \in B \rbrace \rightarrow CD=B \ \ \ \ \ (2)$

Definição 3 Chama-se imagem da função ${ f }$ , o conjunto ${ Im }$ formado por todos elementos ${ y }$ de ${ B }$ pelos os quais existe ${ x }$ em ${ A }$ . O conjunto de imagem ${ Im }$ é subconjunto do contradomínio ${ CD }$ Matematicamente, temos:

$\displaystyle Im(f) \subset CD (f) \ \ \ \ \ (3)$

Vamos explicar por diagrama, temos:

— 2. Determinação do domínio, do contradomínio e da imagem da função —

Exercício 1 Determinar o domínio, o contradomínio e a imagem da função.

Resolução

-O domínio é ${ D(f)=A=(-2,-1,0) }$

-O contradomínio é ${ CD(f)=B=(-3,-2,-1,0,3) }$

-A Imagem é ${ Im(f)=(-2,-1,3) }$

Exercício 2

Seja a função ${ f=2x-1 }$ de ${ A=(0,1,4,5) }$ em ${ B=(-1,0,1,2,3,5,7,9)}$ ,com ${ x\in A }$ e ${ y\in B }$ ,

determinar o domínio, o contradomínio e a imagem.

Resolução

– O domínio é ${ D(f)=A=(0,1.4,5) }$

– O contradomínio é ${ CD(f)=B=(-1,0,1,2,3,5,7,9) }$

– A imagem será determinada atribuindo a variável ${ x }$ todos os valores do domínio na lei dada, os seus resultados serão as imagens.

logo, temos:

Para ${ x=0 }$ , temos: ${ f(0)=2(0)-1 \leftrightarrow f(0)=0-1 \leftrightarrow f(0)=-1 }$

Para ${ x=1 }$ , temos: ${ f(1)=2(1)-1 \leftrightarrow f(0)=2-1 \leftrightarrow f(0)=1 }$

Para ${ x=4 }$ , temos: ${ f(4)=2(4)-1 \leftrightarrow f(4)=8-1 \leftrightarrow f(0)=7 }$

Para ${ x=5 }$ , temos: ${ f(5)=2(5)-1 \leftrightarrow f(5)=10-1 \leftrightarrow f(5)=9 }$

logos, os resultados ou os valores numéricos que determinamos são as imagens. O conjunto é ${ Im(f)=(-1,1,7,9) }$

Vamos ilustrar por diagrama o que acabamos de determinar:

As imagens são todos os elementos do contradomínio ( ${ CD=B }$ ) indicados pela seta. Assim, temos: ${ Im=(-1,1,7,9) }$

Exercício 3

Determinar o domínio, o contradomínio e a imagem da função:

Resolução

– O domínio da função é: ${ D(f)=A=(-4,-2,0,2) }$

– O contradomínio é igual a imagem: ${ CD=Im=(-1,1,4,5) }$

O contradomínio é igual a imagem porque todos os elementos de contradomínio têm ligação com os elementos do domínio como ilustra a figura a cima.

Exercício 4

Seja a relação ${ f:\mathbb{R \rightarrow \mathbb{N}} }$ definida por ${ f(x)=x^{2}+x-2 }$ ,

determinar:

${ a) }$ O domínio;

${ b) }$ O contradomínio;

${ c) }$ A imagem dos elementos do domínio ${-3 }$ e ${ -1 }$

Resolução

${ a) }$ ${ D(f)=\mathbb{R}}$ claramente.

${ b) }$ ${ CD(f)=\mathbb{N}}$ claramente.

${ c) }$ Segundo a terceira definição, a imagem deve ser um elemento do contradomínio.

Analisando, temos:

Para ${ x=-3 }$ , temos: ${ f(-3)=(-3)^{2}-3-2 \leftrightarrow f(-3)=9-5 \leftrightarrow f(-3)=4}$ .

Como ${ 4\in \mathbb{N}}$ , então é a imagem de ${ -3 }$

Para ${ x=-1 }$ , temos: ${ f(-1)=(-1)^{2}-1-2 \leftrightarrow f(-1)=1-3 \leftrightarrow f(-2)=-2 }$ .

Como ${ -2\notin \mathbb{N}}$ , então não é a imagem. ou seja ${ -1 }$ não tem imagem.

como ${ -1 }$ é um elemento do domínio e não tem imagem, então a relação dada nesse caso, também não define a função.

Obs:O leitor terá que ler a matéria de conceito de função disponível nesse mesmo blog.

Exercício 5

Dada a função ${ f:\mathbb{R}\rightarrow \mathbb{R}}$ de definida por
${ \left.f(x)=\lbrace \begin{array}{ll} x^2-3 & se \ x\in \mathbb{Z};\\ \dfrac{x-3}{3} & se \ x\notin \mathbb{Z} \end{array} \right. }$

Determinar:

${ a) }$ o domínio;

${ b) }$ O contradomínio;

${ c) f(-6) }$ ;

${ d) f(\dfrac{3}{2}) }$ ;

${ e) f(0,1)}$ ;

${ f) f(2) }$

Resolução

${ a) }$ ${D(f)=\mathbb{R}}$ é evidente.

${ b)}$ ${ CD(f)=\mathbb{R}}$ é evidente.

${ c) }$ Como ${ -6\in\mathbb{Z} }$ , temos: ${ f(-6)=-6+2 \leftrightarrow f(-6)=-4 }$ .

${ d)}$ Como ${ \dfrac{3}{3}\notin\mathbb{Z} }$ ,temos: ${ f(\dfrac{3}{2})=(\dfrac{3}{2})^2 \leftrightarrow f(\dfrac{3}{2})=\dfrac{9}{4} }$ .

${ e) }$ como ${ 0,1\notin\mathbb{Z}}$ , temos: ${ f(0,1)=(0,1)^2 \leftrightarrow f(0,1)=0,01 }$

${f) }$ Como ${ 2\in\mathbb{R} }$ , temos: ${ f(2)=2+2 \leftrightarrow f(2)=4 }$

Exercício 6

Na função real ${ f(x)=x+1 }$

Resolução

Como a função é real então ${ x\in\mathbb{R} }$ , então ${ f(x)=-3 }$ . Temos: ${ -3=x+1 \leftrightarrow x+1=-3 \leftrightarrow x=-3-1 \leftrightarrow x=-4 }$

${ -3=x+4 \leftrightarrow x+4=-3 \leftrightarrow x=-3-4 \leftrightarrow x=-7 }$ logo os elemento do domínio são: ${ -7 }$ e ${ -4 }$

Exercício 7

Na função real ${ \left.f(x)=\lbrace \begin{array}{ll} x+2 & se \ x<2;\\ x^2 & se \ x\geq 2 \end{array} \right. }$ determinar o elemento do domínio cuja imagem é ${ 6 }$

Resolução

Como a função é real então ${ x\in\mathbb{R} }$ e como ${ 6 }$ é imagem da função, temos: ${ f(x)=6 }$ .

Temos:

${ 6=x^2-3 \leftrightarrow x^2-3=6 \leftrightarrow x^2=6+3 \leftrightarrow x^2=9 \leftrightarrow x=\pm 3 \Longleftrightarrow x_{1}=3}$ não satisfaz porque não está no intervalo ${ x<2 }$ e ${x_{2}=-3 }$ satisfaz porque está ao intervalo referido.

${ 6=\dfrac{x-3}{3} \leftrightarrow \dfrac{x-3}{3}=6 \leftrightarrow x-3=18 \leftrightarrow x=21}$ satisfaz porque está no intervalo definida pela própria função dada que é ${ x\geq 2 }$

logo os elemento do domínio são: ${ -3 }$ e ${ 21 }$

— 3. Determinação da imagem da função quadrática —

Dada a função geral, ${ f(x)=ax^2+bx+c }$

se ${ a>0 }$ a imagem será ${ Im=\lbrace y\in \mathbb{R}\vert y\geq\dfrac{-\vartriangle}{4a}\rbrace }$

se ${ a<0 }$ a imagem será ${ Im=\lbrace y\in \mathbb{R}\vert y\leq\dfrac{-\vartriangle}{4a}\rbrace }$

Exercício 8

Determinar a imagem da função ${ f(x)=x^2+x-20}$ definida ${ \mathbb{R} }$ .

Resolução

${f(x)=x^2+x-20}$ é a função dada, então temos:

Primeiro, vamos determinar os coeficientes ${ a=1 }$ , ${ b=1 }$ e ${ c=-20 }$

segundo, vamos determinar o ${ \vartriangle }$

${\vartriangle=b^2-4ac \leftrightarrow \vartriangle=(1)^2-4(1)(-20) \leftrightarrow \vartriangle=81 }$

Por fim, temos: ${ \dfrac{-\vartriangle}{ 4a} }$ ${ = \dfrac{-81}{4}}$

Como ${ a=1 \rightarrow a>0 }$ , logo:

${ Im=\lbrace y\in \mathbb{R}\vert y \geq \dfrac{-81}{4} \rbrace }$

Exercício 9

Determinar a imagem da função ${ f(x)=-3x^2+6x+3}$ definida em ${ \mathbb{R}}$ .

Resolução

${f(x)=-3x^2+6x-3}$ é a função dada, então temos:

Primeiro, vamos determinar os coeficientes ${ a=-3 }$ , ${ b=6 }$ e ${ c=-3 }$

Segundo, vamos determinar o ${ \triangle }$

${\vartriangle=b^2-4ac \leftrightarrow \vartriangle=(6)^2-4(-3)(3) \leftrightarrow \vartriangle=72 }$

Por fim, temos: ${ \dfrac{-\vartriangle}{4a} }$ ${ = \dfrac{-72}{-12}=6}$

Como ${ a=-3 \rightarrow a<0 }$ , logo: ${ Im=\lbrace y\in \mathbb{R}\vert y \leq 6 \rbrace }$

Exercício 10 Determinar ${ k }$ na função ${ f(x)=2x^2-5x+k }$ definida em ${ \mathbb{R} }$ para que a imagem seja ${ Im=\lbrace y\in \mathbb{R}\vert y\geq \dfrac{7}{8} \rbrace }$

Resolução

Vamos começar da seguinte maneira:

Como ${ Im=\lbrace y\in \mathbb{R}\vert y\geq \dfrac{7}{8}\rbrace \rightarrow \dfrac{-\vartriangle}{4a}=\dfrac{7}{8}}$ .

Como ${ a=2 }$ , ${ b=-5 }$ e ${ c=k }$ , Calculando o ${ \vartriangle }$ , temos:

${ \vartriangle=(-5)^2-4(2)(k) \leftrightarrow \vartriangle=25-8k}$

Substituir ${ a=2 }$ e a expressão anterior na igualdade ${\dfrac{-\vartriangle}{4a}=\dfrac{7}{8} }$ ,

temos: ${\dfrac{-25+8k}{8}=\dfrac{7}{8} \leftrightarrow -25+8k=-7 \leftrightarrow 8k=32 \leftrightarrow k=4 }$

DOMÍNIO DE FUNÇÃO

08/01/2015 12:23 am / 3 comentários em DOMÍNIO DE FUNÇÃO

Definição 1

Seja a função ${y=f(x)}$ de ${A}$ em ${B}$ . ${ D }$ é o domínio da função, ao conjunto de todos os elemento de ${ x \in A }$ pelos os quais existe ${ y \in B }$ .

Matematicamente, temos:

$\displaystyle D=\lbrace x\in \mathbb{R}\mid \forall x \in A, \exists y \in B \rbrace \rightarrow D=A \ \ \ \ \ (1)$

Exercício 1 Seja a função ${ f(x)=x^2 +2x-1}$ de ${ A=(-2,0,1,2,3)}$ e ${ B=(-1,0,1,3,4,14, 20,23)}$ , determinar o seu domínio.

Resolução

O domínio dessa função é ${ D=A \rightarrow D=(-2,0,1,2,3) }$ .

Definição 2 Dada a função ${y=f(x)}$ . Chama-se domínio ao conjuntos de valores reais de ${ x }$ para os quais a função está definida.

Em símbolos, temos:

$\displaystyle D=\lbrace x\in \mathbb{R}\mid \forall x \in A, \exists y \in B \rbrace \ \ \ \ \ (2)$

No parágrafo a seguir, entenderemos melhor essa definição

— 1. Determinação de domínio de diversas funções —

Segundo a definição, antes de determinarmos o domínio de uma função dada devemos, em primeiro passo, estudar a natural da função assim como a sua definição.

Vamos apresentar algumas formas de representação de domínio:

${ D=\lbrace x\in \mathbb{R} \mid g(x)\neq 0 \rbrace }$

${ D= \mathbb{R}- \lbrace g(x)= 0 \rbrace }$

${ D= \mathbb{R}/\lbrace g(x)= 0 \rbrace }$

${ D=\lbrace x \in \mathbb{R}\vert a\leq x \leq b \rbrace }$

${ D=\lbrace x \in \mathbb{R}\vert a < x < b \rbrace }$

${ D=\lbrace x \in \mathbb{R}\vert a\leq x < b \rbrace}$

${ D=\lbrace x \in \mathbb{R}\vert a < x \leq b \rbrace }$

ou simplesmente ${ D=\mathbb{R} }$

${ \forall a \in \mathbb{R} }$ e ${ \forall b \in \mathbb{R} }$

Essas representações dependem do critério do leitor outras do tipo de função em causa.

Vamos agrupar as funções segundo as suas definições para facilitar a compreensão do leitor e posteriormente podermos resolver as funções de expressões mistas.

— 2. Domínio da função polinomial —

Definição 3 O domínio da função polinomial é sempre o conjunto dos números reais

Em símbolos, temos:

$\displaystyle f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots+a_{0} \ \ \ \ \ (3)$

${ D=\mathbb{R}}$

Exercício 2

Determinar o domínio da função ${f(x)=2x-3}$

Resolução:
O domínio é ${ D=\mathbb{R} }$
Quando se trata de um polinómio o domínio é imediatamente o conjunto dos números reais ou simplesmente ${ \mathbb{R} }$

Exercício 3 Determinar o domínio da função ${f(x)=\dfrac{3}{5}x^{5}+7x^{4}-3x^{3}+x^{2}+6x+11}$

Resolução:
${ D=\mathbb{R} }$ , Claramente.

Exercício 4 Determinar o domínio da função ${f(x)=k }$ onde ${ k\in \mathbb{R} }$

Resolução:
Como ${ k }$ é qualquer número real, então o domínio é o conjunto dos números reais ${ (\mathbb{R}) }$

— 3. Domínio de função racional —

Definição 4 O domínio da função racional está definida para o denominador diferente de zero.

Em símbolos, temos:

$\displaystyle f(x)=\dfrac{h(x)}{g(x)} \leftrightarrow g(x)\neq0 \ \ \ \ \ (4)$

${ D=\lbrace x\in \mathbb{R} \mid g(x)\neq 0 \rbrace }$ .

Exercício 5 Determinar o domínio da função ${ y=\dfrac{x-1}{x+2} }$ .

Resolução:
Vamos igualar o denominador a diferente de zero, assim: ${ x+2\neq 0 }$
Agora, vamos resolver:
Temos: ${ x+2\neq 0 \leftrightarrow x\neq-2 }$
logo o domínio é ${ D=\lbrace x\in R\mid x\neq -2 \rbrace }$ ou ${ D= \mathbb{R}-\lbrace-2\rbrace }$

Exercício 6 Determinar o domínio da função ${ y=\dfrac{1}{x^2-3x-4} }$ .

Resolução:
Vamos resolver ${ x^2-3x-4\neq0}$ resolvendo temos: ${x_{1}\neq-1,\ e \ x_{2}\neq4 \rightarrow D= \mathbb{R}-\lbrace-1,4\rbrace }$ ou ${ D=\lbrace x\in R\mid x\neq-1 \ e \ x\neq4 \rbrace }$

— 4. Domínio da função irracional de índice ímpar —

Definição 5 O domínio de uma função irracional de índice ímpar é sempre o conjunto dos números reais.

Em símbolos, temos:

$\displaystyle f(x)=\sqrt[2k-1]{g(x)} \ \ ( \forall k\in\mathbb{N}) \rightarrow D=\mathbb{R} \ \ \ \ \ (5)$

${ D=\mathbb{R} }$

Exercício 7 Determinar domínio da função ${f(x)=\sqrt[3]{x^4 -\dfrac{5}{2} x+3}}$

Resolução:
Evidentemente que ${D=\mathbb{R}}$

Exercício 8 Determinar domínio da função ${f(x)=\sqrt[7]{-2x^2 +x}+9}$

Resolução:
Claramente que ${D=\mathbb{R}}$

— 5. Domínio de função irracional de índice par —

Definição 6 O domínio da função irracional de índice par estás definida para o radical maior ou igual a zero.

Em símbolos, temos:

$\displaystyle f(x)=\sqrt[2k]{g(x)} \ \ k \in \mathbb{N} \ \ \ \ \ (6)$

${ D=\lbrace x\in \mathbb{R}\mid g(x)\geq0\rbrace }$

Exercício 9 Determinar o domínio da função ${ f(x)=\sqrt{3x+12}}$ .

Resolução:
${ 3x+12\geq0 \rightarrow 3x\geq-12 \leftrightarrow x\geq-\dfrac{12}{3} \leftrightarrow x\geq-4 }$ , logo o domínio é,

${ D=\lbrace x\in \mathbb{R}\mid x\geq-4\rbrace }$

Exercício 10 Determinar o domínio da função ${ f(x)=\sqrt[4]{x^2+5x+6}}$ .

Resolução:
${ x^2+5x+6\geq0 }$ resolvendo temos: ${ x\leq -3 }$ ou ${ x\geq -2 }$ , logo o domínio é: ${D=\lbrace x\in \mathbb{R}\mid x\leq -3 \ e \ x\geq-2\rbrace }$ .

— 6. Domínio de função logaritmica —

Definição 7 O Domínio da função logarítmica é definido, para logaritmando igual ou maior que um e a base maior que zero e diferente de um.

Em símbolos, temos:

$\displaystyle f(x)=\log_{a}^x \ \ \ \ \ (7)$

${ D=\lbrace x\in \mathbb{R}\mid 0<a<1 \ \ e \ \ a>1 \ e \ x>0 \rbrace}$

Exercício 11 Determinar o domínio da função ${ f(x)=\log_{4}^{(4x^2-3x-1)}}$ .

Resolução:
${4x^2-3x-1>0}$ Primeiro vamos determinar as raízes, temos: ${ x_{1}=1}$ ou ${ x_{2}=-\dfrac{1}{4} }$ . Como se trata de inequação, o intervalo que satisfaz é: ${ x_{2}<-\dfrac{1}{4} \ e \ x>1 }$ assim o domínio da função é: ${ D=\lbrace x \in \mathbb{R}\mid x_{2}<-\dfrac{1}{4} \ e \ x>1 \rbrace }$

Exercício 12 Determinar o domínio da função ${ y=\log_{(x-2)}^7}$ .

Resolução:
${ 0<x-2<1 }$ e ${ x-2>1}$ segundo a condição da base do logaritmo.
vamos resolver: ${ 0<x-2<1 \leftrightarrow 0+2<x<1+2 \leftrightarrow 2<x<3}$
Outra condição: ${ x-2>1 \rightarrow x>1+2 \leftrightarrow x>3 }$
Temos o domínio ${ D=\lbrace x \in\mathbb{R}\mid 2<x<3 \ e \ x>3\rbrace }$

Exercício 13 Determinar o domínio da função ${ y=\log_{(x+3)}^{x^2-x}}$ .

Resolução:
temos: ${x^2-x>0 \rightarrow x(x-1)>0 \leftrightarrow x>0}$ e ${ x-1>0 \leftrightarrow x>1}$ ou ${ x<0 }$ e ${ x-1<0 \leftrightarrow x<1 }$
A propriedade da base: ${ 0<3+x<1 \rightarrow -3<x<-2 }$ e ${ x+3>1 \leftrightarrow x>-2 }$
achando a intersecção de todas as condições temos: ${ -2<x<0 }$ e ${ x>1 }$
o domínio é ${ D=\lbrace x \in\mathbb{R}\mid -2<x<0 \ \ e \ \ x>1\rbrace }$

— 7. Domínio de função exponencial —

Definição 8 O domínio da função exponencial é definido para base maior que zero e diferente um.

Em símbolos, temos:

$\displaystyle f(x)=a^x \ \ \ \ \ (8)$

${ D=\lbrace a \in \mathbb{R}\vert a>0 \wedge a \neq 1 \rbrace }$

Exercício 14 Determinar o domínio da função ${ y=2^x }$
Resolução:
Claramente que o ${ D=\mathbb{R} }$

Exercício 15 Determinar o domínio da função ${ y=(\dfrac{1}{3} )^{\dfrac{x-1}{4}} }$

Resolução:
Sem mais comentário o domínio é ${ D=\mathbb{R} }$

— 8. Domínio de função trigonométrica —

Definição 9 – O domínio da função de seno é o conjunto dos números reais. Em símbolos, temos:

$\displaystyle y = \sin x \ \ \ \ \ (9)$

O domínio é ${ D=\mathbb{R} }$

Definição 10 – O domínio da função de cosseno é o conjunto dos números reais. Em símbolos, temos:

$\displaystyle y = \cos x \ \ \ \ \ (10)$

O domínio é ${ D=\mathbb{R} }$

Definição 11 – O domínio da função de tangente é definido para cosseno diferente de zero. Em símbolos, temos:

$\displaystyle y = \tan x \ \ \ \ \ (11)$

${ D=\lbrace \forall x \in \mathbb{R}\vert \cos x \neq 0 \rbrace }$ ${ \rightarrow D=\lbrace x \in \mathbb{R}\mid x\neq\dfrac{\pi}{2}+k\pi \rbrace }$

Exercício 16 Determinar o domínio da função ${ y=\tan\dfrac{x}{2}}$

Resolução: Sabemos que a tangente não está definida para ${ \dfrac{\pi}{2} }$ então, temos: ${ \tan\dfrac{x}{2}\neq\tan\dfrac{\pi}{2} \leftrightarrow \dfrac{x}{2}\neq\dfrac{\pi}{2}+k\pi }$ ${ \leftrightarrow x\neq \pi+2k\pi }$ . logo o domínio é: ${ D(x)=\lbrace x\in \mathbb{R}\mid x\neq \pi+2k\pi \rbrace }$

Exercício 17 Determinar o domínio da função ${ f(x)=\dfrac{1+\cot x}{1-\tan x} }$ .

Resolução: Destaca-se a condição da ${\cot x, \tan x }$ e a condição do denominador ${1-\tan x }$
– A Condição da ${\cot x }$ : ${\cot x \neq \cot 0 \leftrightarrow x \neq k\pi }$
– A Condição da ${\tan x }$ : ${ \tan x \neq \tan \dfrac{\pi}{2} \leftrightarrow x\neq \dfrac{\pi}{2}+k \pi}$
– A Condição do denominador ${ 1-\tan x }$ : ${ 1-\tan x \neq0 \leftrightarrow \tan x \neq1 \leftrightarrow \tan x \neq\tan\dfrac{\pi}{4}}$ ${ \leftrightarrow x \neq \dfrac{\pi}{4}+k\pi }$
Finalmente, temos: ${ D=\lbrace x\in \mathbb{R}\mid x \neq k\pi \ e \ x\neq \dfrac{\pi}{2}+k \pi \ e \ x \neq \dfrac{\pi}{4}+k\pi\rbrace}$

— 9. Determinação de domínio de diversas funções —

Exercício 18 Determinar o domínio da função ${ y=\dfrac{1}{\sqrt[3]{3x+5}}}$
Resolução:
Como o índice é ímpar vamos analisar a condição só do denominador.
${ 3x+5\neq0\Longleftrightarrow x=\dfrac{-5}{3}}$ , logo o domínio é, ${ D=\lbrace x \in\mathbb{R}\mid x\neq-\dfrac{5}{3}\rbrace }$ .

Exercício 19 Determinar o dominio da função ${ f(x)=\dfrac{x^2-1}{\sqrt{x}-2} }$

Resolução:
Nesse exercício temos que impor a condição do denominador e do radical porque o índice é par.
-A condição do radical: ${ x\geq0 }$
-A condição do denominador: ${ \sqrt{x}-2 \neq0 \rightarrow \sqrt{x}\neq2 \rightarrow x\neq4 }$
-Intersecção das duas condições: ${ 0\leq x<4 \ e \ 4<x }$
finalmente o domínio é: ${ D=\lbrace x \in \mathbb{R} \mid 0 \leq x<4 \ e \ 4<x \rbrace }$

Exercício 20 Qual é o domínio da função ${ f(x)=\dfrac{1}{\log^{x}} }$ ?
Resolução:
Nesse exercício temos a condição do denominador e do logatitmando porque o índice é par.
-A Condição do logaritmando é: ${ x>0 }$
-A Condição do denominador é : ${ \log^{x}\neq0 \rightarrow x\neq10^0 \rightarrow x\neq1 }$
finalmente o domínio é: ${ D=\lbrace x \in\mathbb{R}\mid 0<x<1 \ e \ x>1\rbrace}$ .

Exercício 21 O domínio da função ${ f(x)=\log(\sin x)}$ é?

Resolução:
Nesta função está em caso, simplesmente, a condição do logaritmando.
Temos: ${\sin x >0 \leftrightarrow 0< x < \pi \leftrightarrow D=\lbrace x \in\mathbb{R}\mid 0 < x < \pi \rbrace}$

Exercício 22 Ache o domínio da função ${ y=\dfrac{2+\sqrt{x-5}}{x^2-64} }$ .
Resolução:
Vamos estudar a condição do radical e do denominador.
– A Condição do denominador: ${ x^2-64\neq0 \leftrightarrow x^2\neq64 \leftrightarrow x\neq\pm8 }$
– A Condição do radical ${ x-5\geq \leftrightarrow x\geq5}$
– Intersecção das duas condições resulta ${ 5\leq x < 8 \ e \ x>8 }$ :
finalmente o domínio é: ${D=\lbrace x \in\mathbb{R}\mid 5\leq x < 8 \ e \ x>8 \rbrace }$

Exercício 23 Encontre o domínio da função ${ f(x)=\dfrac{\sqrt{x-1}}{x^3}+\dfrac{2x}{\sqrt{x+4}} }$ .
Resolução:
– A condição ${\sqrt{x-1} \leftrightarrow x-1\geq0 \leftrightarrow x\geq1 }$
– A condição ${ x^3\neq0 \Longrightarrow x\neq0 }$
– A condição do denominador ${\sqrt{x+4}\neq0 \leftrightarrow x+4>0 \leftrightarrow x>-4 }$
A intersecção das três condições fornece-nos o seguinte resultado: ${ x>1 }$ , logo o domínio da função é:
${ D=\lbrace x \in \mathbb{R}\mid 1\leqslant x \rbrace }$

Exercício 24 Determinar o domínio da função ${ f(x)= \sqrt{2^{(x-2)}-1} }$ .
Resolução: ${ f(x)= \sqrt{2^{(x-2)}-1} }$ isto só é possível para ${ 2^{(x-2)}-1\geq0 }$ . logo temos: ${ 2^{(x-2)} \geq 1 \leftrightarrow 2^{(x-2)} \geq 2^0 }$ ${ \leftrightarrow x-2 \geq 0 \leftrightarrow x \geq 2 }$ Por fim temos o domínio: ${ D= \lbrace x \in \mathbb{R} \mid 2\leq x \rbrace }$ .

Exercício 25 Dada a função ${ f(x)=\dfrac{1}{\vert x-2 \vert -3} }$ . Determinar o domínio.

Resolução:

O denominador diferente de zero: ${ \vert x-2\vert-3\neq0 \leftrightarrow \vert x-2 \vert \neq3 }$ , segundo as propriedades modular, temos:
– ${ x-2 \neq3 \leftrightarrow x\neq5 }$
– ${ x-2 \neq-3 \leftrightarrow x\neq-1 }$
Assim o domínio é ${ D=\mathbb{R}-(-1, 5) }$

CONCEITO DE FUNÇÃO

07/25/2015 1:09 am / Deixe um comentário

— 1. Conceito de funções —

Definição 1

Sejam dois conjuntos ${A}$ e ${B}$ , ambos diferentes do conjunto vazio e ${f}$ uma relação de ${A}$ em ${B}$ , diz-se que ${f}$ é uma função definida de ${A}$ em ${B}$ se, e somente se, para todo ${x}$ que pertence ao conjunto ${A}$ existe um, e só um elemento ${y}$ que pertence ao conjunto ${B}$ de maneira que o par ordenado ${(x,y)}$ pertença a função ${f}$ .

Em simbolos, temos:

${ f }$ é uma função de ${ A }$ em ${ B }$

$\displaystyle \leftrightarrow \forall_x \in A,\exists y \in B \ tal \ que \ (x,y) \in f . \ \ \ \ \ (1)$

Nota: podemos dizer que ${ f }$ é uma função ou ${ f }$ é uma aplicação.

Exercício 1 Dados os conjuntos ${A= (-2, 1, 2, 3) }$ e ${ B=(-2,-1,1,5,6,13)}$ e a seguinte relação ${ D= \lbrace(x,y)\in A \times B \mid y=( x+1)^2 -3 \rbrace}$ de ${A}$ em ${B}$ . É uma função? Resolução

Vamos começar a resolver: Como ${ x \in A }$ segundo a definição, então temos:

Para ${x=-2}$ , temos ${ y=( x+1)^2 -3\rightarrow y=( -2+1)^2 -3\rightarrow y=-2\rightarrow y\in B }$ , logo ${(-2,-3)\in f }$ .

Para ${x=1}$ , temos ${y=( x+1)^2 -3\rightarrow y=( 1+1)^2 -3\rightarrow y=1\rightarrow y\in B }$ , logo ${(1,1)\in f }$ .

Para ${x=2}$ , temos ${y=( x+1)^2 -3\rightarrow y=( 2+1)^2 -3\rightarrow y=6\rightarrow y\in B }$ , logo ${(3,6)\in f }$ .

Para ${x=3}$ , temos ${ y=( x+1)^2 -3\rightarrow y=( 3+1)^2 -3\rightarrow y=13 \rightarrow y \in B }$ , logo ${(3,13)\in f}$ . como todos elementos de ${A}$ correspondem a um, e só um elemento de ${B}$ , então a relação ${D= \lbrace(x,y) f \rbrace \in A \times B \mid y=( x+1)^2 -3 \rbrace}$ é uma função.

Exercício 2 Dados os conjuntos ${ A=\lbrace 0,1,3,4,5\rbrace }$ e ${ B=\lbrace x\in \mathbb{R} \mid 1\leq x\leq 2\rbrace }$ pela lei de transformação ${y=\dfrac{x+3}{x+2}}$ . Mostre que é uma função de ${A}$ em ${B}$ . Resolução: Como ${x}$ é do conjunto ${A}$ , então temos:

Para ${ x=0 \rightarrow y=\dfrac{0+3}{0+2} \rightarrow y=\dfrac{3}{2} \rightarrow y\in B\rightarrow (0,\dfrac{3}{2})\in f }$ . Para ${ x=1 \rightarrow y=\dfrac{1+3}{1+2} \rightarrow y=\dfrac{4}{3}\rightarrow y\in B\rightarrow (1,\dfrac{4}{3})\in f }$ .

Para ${ x=3\rightarrow y=\dfrac{3+3}{3+2} \rightarrow y=\dfrac{6}{5}\rightarrow y\in B\rightarrow (3,\dfrac{6}{5})\in f}$ .

Para ${ x=4 \rightarrow y=\dfrac{4+3}{4+2} \rightarrow y=\dfrac{7}{6} \rightarrow y\in B\rightarrow (4,\dfrac{7}{6})\in f}$ .

Para ${ x=5 \rightarrow y=\dfrac{5+3}{5+2} \rightarrow y=\dfrac{8}{7} \rightarrow y\in B\rightarrow (5,\dfrac{8}{7})\in f}$ .

vimos que todos elementos do conjunto ${A}$ correspondem a um, e somente um elemento do conjunto ${B}$ , então ${y=\dfrac{x+3}{x+2}}$ é uma aplicação de ${A}$ em ${B}$ .

Exercício 3 Seja a relação ${ f(x)=26-x^2 }$ aplicada de ${ A }$ em ${ \mathbb{N}}$ , onde ${ =\lbrace x\in \mathbb{R}\mid x\leq0\rbrace }$ , mostre que não é uma aplicação de ${A}$ em ${ \mathbb{N} }$ Resolução: Vamos lá resolver esse exercício:

Segundo a linguagem do exercício, garante-nos, seguramente, que não é uma função(ou não é uma aplicação) de ${A}$ em ${\mathbb{N}}$ , logo temos que provar que existe um elemento ${x}$ do conjunto ${A}$ que não corresponde a um elemento ${y}$ do conjunto ${\mathbb{N}}$ ou,que corresponde mais de um elemento de conjunto ${\mathbb{N}}$ .

Como o conjunto de partida ${A}$ é infinito, o processo que fizemos nos exemplos anteriores é trabalhoso demais que é, analisar um elemento por cada elemento correndo risco de fazê-lo ${-l0 }$ cem vezes. Sendo assim, é suficiente mostrar que existe um elemento ${x}$ de ${A}$ que não corresponde a ${y}$ de ${\mathbb{N} }$ ou, que corresponde mais de um elemento de ${\mathbb{N}}$ . Temos:

Para ${ x=-6 \rightarrow f(6)=26-(-6)^2 \rightarrow f(6)=26-36 \rightarrow f(6)=-10 }$ Como ${-10}$ não pertence ao conjunto dos números natural ${ \mathbb{N} }$ , implica que ${ f(x)=26-x^2}$ não é uma função ${A}$ em ${ \mathbb{N}}$ .

Exercício 4 Dados os conjuntos ${ A=(-2, 1, 2, 3)}$ e ${B=(-2,1,4,5,7,9)}$ definida por ${y=-2x+3}$ de ${A}$ em ${B}$ . É uma função?

Resolução: Como ${x \in A }$ , então temos:

Para ${ x=-2 \rightarrow y=-2x+3 \rightarrow y=4+3 \rightarrow y=7 \rightarrow y \in B }$ , logo ${(-2,7)\in f}$ .

Para ${x=1}$ , temos ${ y=-2x+3 \rightarrow y=-2+3\rightarrow y=1\rightarrow y\in B}$ , logo ${(1,1) \in f }$ .

Para ${ x=2 }$ , temos ${y=-2x+3\rightarrow y=-4+3\rightarrow y=-1}$ , ${y}$ não pertence a função.

Como existe um elemento do conjunto ${ A}$ que não corresponde a nenhum elemento de ${B}$ , então a relação dada não é uma função de ${A}$ em ${B}$ . Não precisas terminar o processo, basta indicar um elemento do conjunto ${ A }$ cujo resultado não é de ${ B }$ é suficiente dizer que não é uma função.

Exercício 5 Seja a relação ${ y^2 =(x-2)^2 +x }$ de ${\mathbb{R}^+}$ em ${\mathbb{R}}$ . Mostre se é uma aplicação.

Resolução:

Vamos mostrar ao contrário que não é uma aplicação, isto equivale dizer, existe um elemento ${x}$ de ${\mathbb{R}^+}$ que não se relaciona com um, ou que se relaciona com mais de um elemento ${y}$ de ${\mathbb{R}}$ . A relação ${y^2 =(x-2)^2 +x }$ de ${\mathbb{R}^+}$ em ${\mathbb{R}}$ para ${x=3}$ ,temos: ${ y^2 =(3-2)^2 +3 \rightarrow y^2 =(1)^2 +3 \rightarrow y^2 =1+3 \rightarrow y^2 =4 \rightarrow y=\pm2}$ , logo não é uma função porque para ${3}$ de ${ \mathbb{R}^+ }$ , existem ${ -2 }$ e ${ 2 }$ em ${\mathbb{R}}$ . Apenas um elementos em ${\mathbb{R}}$ neste caso.

Exercício 6 A relação ${ f(x)=\frac{x^3}{3} }$ é uma função de ${A}$ em ${\mathbb{R}}$ , onde ${ A=\lbrace x\in\mathbb{R}\mid -2\leq x \leq2\rbrace}$ ? Resolução:

Como é impossível numerar os elementos do conjunto ${A}$ é mais fácil provar ao contrário que não é uma aplicação indicando um elemento de ${A}$ que não resulta um elemento de ${\mathbb{R} }$ ou que resulta dois ou mais elementos de ${\mathbb{R}}$ .

É evidente que não existe nenhum elemento de ${A}$ cujo o resultado de ${f(x)}$ não seja real ou seja, para todos os elementos de ${A}$ existe, claramente, um numero real, por isso é uma aplicação ou é uma função de ${A}$ em ${ \mathbb{R}}$ .

Exercício 7 Dados os conjuntos ${ A= (-2, 1, 2, 3) }$ e ${ B=(-3 ,-2,-1,1,4,5,6,9)}$ e a lei definida por ${ C= \lbrace(x,y)\in A \times B \mid y=7-x \rbrace }$ de ${A}$ em ${B}$ , prove se é uma função.

Resolução:

Como ${ x \in A }$ , então temos:

Para ${ x=-2 }$ , temos ${y=7-x\rightarrow y=7+2 \rightarrow y=9 \rightarrow y \in B }$ , logo ${(-2,9)\in f }$ .

Para ${ x=1 }$ , temos ${ y=7-x \rightarrow y=7-1 \rightarrow y=6 \rightarrow y\in B }$ , logo ${(1,6) \in f }$ .

Para ${ x=2 }$ , temos ${ y=7-x\rightarrow y=7-2 \rightarrow y=5\rightarrow y\in B }$ , logo ${(2,5)\in f }$ .

Para ${ x=3 }$ , temos ${ y=7-x\rightarrow y=7-3 \rightarrow y=4\rightarrow y\in B }$ , logo ${(3,4)\in f }$ . Vimos que para todos elementos de ${x}$ que pertencem ao conjunto ${A}$ , pela lei de transformação ${y=7-x}$ , corresponde a um único elemento do conjunto ${B}$ , logo a relação ${ C= \lbrace(x,y)\in A \times B \mid y=7-x \rbrace }$ de ${A}$ em ${B}$ é uma função ou é uma aplicação de ${A}$ em ${B}$ .

Luso Academia

Category Archives: 01 Matemática

Continuidade em Espaços Métricos. Continuação.

Partilhar

Função composta

Partilhar

Domínio contradomínio e imagem de função.

Partilhar

DOMÍNIO DE FUNÇÃO

Partilhar

CONCEITO DE FUNÇÃO

Partilhar