— 6. Introdução à Física Quântica —

Ao contrário do que fizemos nos capítulos anteriores este capítulo fará menção de algumas experiências que motivaram a formulação da Física Quântica. Para além disso as nossas formulações iniciais serão expostas de uma forma menos resumida.

— 6.1. Novos Resultados, Novas Concepções —

Qualquer pessoa que se tenha aproximado de um laboratório e teve que realizar uma experiência sabe que para se poder dizer algo sobre o sistema em estudo é sempre necessário interagir com o sistema. Em linguagem mais respeitável devemos dizer o acto de medição perturba sempre o sistema em estudo.
Para além disso temos também o conceito de estado mecânico. Ora o conceito de estado mecânico pressupõe duas coisas:

1. A perturbação pode, em princípio (nalguns casos), tornar-se tão pequena quanto se queira. O facto de haver sempre limites é uma propriedade dos instrumentos que se utiliza e não da teoria que serve como base.
2. Existem algumas perturbações cujo efeito não pode ser desprezado. No entanto é sempre possível fazer um calculo exacto de quais os efeitos e desse modo é possível compensá-los.

Em suma a teoria que até agora desenvolvemos é causal e determinista.

No entanto uma das duas nuvens negras de Kelvin e mais uns quantos outros resultados experimentais mostraram que uma revisão dos conceitos clássicos era necessária:

• Radiação de corpo negro.
• Efeito fotoeléctrico.
• Princípio da combinação de Ritz.
• Existência e estabilidade de átomos.
• Experiência de Stern-Gerlach.
• Difracção de raios de electrões.
• …

Estes resultados experimentais introduziram as seguintes quebras com o paradigma newtoniano:

• Entidades que tinham uma natureza corpuscular demonstram um comportamento ondulatório.
• Entidades que tinham uma natureza ondulatória demonstram um comportamento corpuscular.
• Existe um carácter estatístico (que parece ser) essencial no comportamento da matéria.
• O carácter atómico da matéria obriga a repensar a natureza do processo de medição: uma vez que existem grandezas cujo valor não pode ser arbitrariamente diminuído uma perturbação tem sempre um valor mínimo que não pode ser melhorado.

— 6.2. A Experiência da Dupla Fenda —

Para tornar mais concreta a discussão anterior vamos olhar com mais cuidado para uma experiência que demonstra muito bem o choque entre as duas concepções que temos vindo a discutir.

— 6.2.1. Duas Fendas e Partículas —

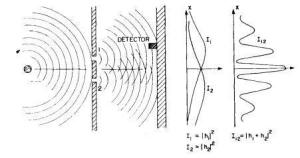
Imaginemos que temos uma situação como a retratada na figura 3 mas desta vez o que incide nas fendas não são ondas mas sim partículas.

Nesta situação as partículas passam pela fenda 1 ou pela fenda 2. As partículas que passam pela fenda 1 são responsáveis pela curva de probabilidades enquanto que as partículas que passam pela fenda 2 são responsáveis pela curva de probabilidades . A curva de probabilidades resultante é simplesmente a soma das curvas e .

— 6.2.2. Duas Fendas e Ondas —

Como já tínhamos visto na secção 3 se fizermos passar uma onda por duas fendas o que se obtém é:

Neste caso a intensidade das ondas é a quantidade que interessa estudar. Temos a curva de intensidades que é causado pela fenda 1 e a curva de intensidades que é causada pela fenda 2. A intensidade resultante no entanto é . O último termo é responsável pela interacção da onda proveniente da fenda 1 com a onda proveniente da fenda 2. Assim sendo é este termo que é responsável pelo padrão de interferência.

— 6.2.3. Duas Fendas e Electrões —

Agora que estamos familiarizados com o comportamento de ondas e partículas vamos estudar o movimento de raios de electrões a passar por duas fendas. Pelo que se sabe dos electrões eles são partículas e como tal esperamos encontrar um comportamento igual ao representado na figura 6. No entanto isto é o que a Natureza tem para nós:

\caption{Experiência de dupla fenda com raios de electrões}

No caso dos electrões temos que novamente pensar em termos de curvas de probabilidades e curvas de probabilidades são inerentes ao conceito de partículas. Contudo o que nós observamos é um padrão de interferências e isso é inerente a ondas…

Para podermos explicar os padrões que vemos temos que assumir que a cada probabilidade está associada uma amplitude de probabilidade . Para calcularmos a probabilidade devemos calcular o módulo quadrado da amplitude de probabilidade . Assim antes de mais devemos calcular a soma da amplitude de probabilidades de passar pela fenda ou de passar pela fenda 2 e só depois devemos calcular o módulo quadrado desta amplitude para obtermos a probabilidade de um electrão passar pela fenda 1 ou de passar pela fenda 2: .

Notar que no parágrafo anterior tratamos o electrão como sendo sempre uma partícula, ainda que seja uma partícula com propriedades muito especiais, e nunca em momento algum o tratamos como sendo uma onda que interfere consigo mesma. Tal tratamento há muito tempo se sabe estar errado, mas, por questões que só podem ser de nostalgia, é frequente encontrá-lo em muitos livros.

— 6.3. Conceitos Básicos e Definições Preliminares —

Após a discussão de alguns dos motivos que levaram os físicos a procurarem um novo paradigma que permitisse fazer sentido do que se passava a nível atómico está na altura de introduzir as nossas habituais definições iniciais.

Definição 40 O estado quântico é definido pela especificação das grandezas físicas relevantes e é representado por uma função que toma valores complexos

Definição 41 O momento linear de uma partícula é representado pelo operador

Definição 42 A energia de uma partícula é representada pelo operador

Definição 43 Para uma partícula livre as seguintes equações são válidas:

— 6.4. Axiomas da Física Quântica —

Os axiomas que aqui vamos apresentar não são os mais gerais nem os mais convenientes para um tratamento maduro da Física Quântica mas são tudo o que necessitamos para cumprir com o âmbito do curso.

Axioma 10 O estado de um sistemas quântico evolui segundo a equação de Schroedinger:

Axioma 11 A probabilidade de que uma partícula seja encontrada no elemento de espaço denota-se por e é:

Axioma 12 Uma partícula quântica é sempre resultante de interferência construtiva.

A função deste axioma é captar de uma só vez a natureza dual do conceito de partícula em Física Quântica.

Axioma 13 O valor médio de uma grandeza física , que se representa , é dado pela seguinte expressão: Onde o integral se calcula na região relevante.

— 6.5. Ondas e Partículas —

— 6.5.4. Radiação de Corpo Negro —

Definição 44 Um corpo negro é um objecto que absorve toda a radiação electromagnética que nele incide.

Para explicar o espectro de radiação de um corpo negro Planck assumiu que a parede de uma cavidade era composta por ressoadores microscópicos que vibravam com frequências diferentes. Cada ressoador tinha a sua frequência própria e devia emitir radiação com essa frequência e com qualquer valor de energia. No entanto Planck postulou que a energia de um ressoador só podia ser . Ou seja que a radiação emitida ou absorvida no interior da cavidade só tomava valores discretos.

Com essa hipótese adicional Planck deduziu uma relação funcional entre a densidade de energia o comprimento de onda da radiação (ou a sua frequência ) e a temperatura a que se encontra o interior da cavidade que se adequa aos dados experimentais:

Recorrendo as equações 6 é possível demonstrar que a potência emitida por unidade de área, , por um corpo negro é .

Também é possível demonstrar que . Sendo

— 6.5.5. Efeito Fotoeléctrico —

Quando se faz incidir luz monocromática sobre uma superfície metálica observa-se que um certo número de electrões se liberta com uma energia muito bem definida. Para além disso sabemos também que existe uma frequência mínima que faz com que electrões se libertem da placa metálica e que o número de electrões libertados aumenta com o aumento da intensidade da luz mas a sua energia cinética não.

No contexto da teoria electromagnética da luz todos estes factos são inexplicáveis. No entanto se assumirmos que a luz se propaga em pacotes discretos de energia (isto é uma generalização enorme da hipótese de Planck que apenas assumiu que trocas de energia se davam de forma discreta) e que estes pacotes de energia são da forma o efeito fotoeléctrico é prontamente explicado.

A energia cinética dos electrões libertados é dada pela expressão onde representa a energia de ligação dos electrões à placa metálica.

— 6.5.6. Átomo de Bohr —

A existência de átomos é segundo o electromagnetismo um acontecimento impossível. Segundo o electromagnetismo partículas carregadas em movimento acelerado deveriam emitir radiação continuamente.

Uma vez que os electrões orbitam em torno do núcleo o seu movimento é claramente acelerado. Assim sendo os electrões deveriam radiar energia continuamente fazendo com que a sua distância ao núcleo fosse cada vez menor até colidirem com o núcleo. Tal, obviamente, não é o que acontece.

Postulando que os electrões só podem orbitar em torno do núcleos em certas trajectórias( recorrendo ao Axioma 12 podemos demonstrar que nestas trajectórias o momento angular do electrão está restringido a ter valores discretos) podemos explicar a estabilidade dos átomos e prever certos fenómenos que sabemos ocorrer ao nível atómico.

Estes estados do electrão em que ele não pode emitir radiação chamam-se estados estacionários. Para transitar de um estado estacionário para outro estado estacionário o electrão deve emitir ou absorver um fotão e a energia deste fotão deve igualar a diferença de energia entre os estados estacionários.

Com estas duas equações é possível prever que os raios permitidos dos electrões são da forma:

Tomando temos o raio menor raio possível (o raio de Bohr) que se denota por .

E que as energias permitidas são da forma

Utilizando as equações 39 e 42 podemos calcular o comprimento de onda do fotão que permite a transição entre estados estacionários

A teoria do átomo de hidrogénio de Bohr também permite explicar o espectro de energia de alguns átomos ionizados.

— 6.5.7. Relação de Incerteza de Heisenberg —

O Axioma 12 diz-nos que para construirmos uma partícula devemos ter um interferência construtiva de ondas. Uma onda é algo que tem uma extensão infinita enquanto que uma partícula não poderia ter uma dimensão mais finita. De modo a obtermos uma partícula através da soma de ondas devemos então somar várias ondas de modo a que a sua soma seja diferente de 0 apenas numa região muito pequena do espaço. Em geral o número de ondas necessário será elevado.

Como cada onda tem o sua comprimento de onda, uma soma de um número elevado de ondas faz com que a partícula resultante tenha um comprimento de onda muito incerto

No limite de somarmos um número infinito de ondas chegamos à situação em que temos uma partícula perfeitamente localizada mas que tem um comprimento de onda totalmente incerto.

Por outra lado se tivermos uma só onda o seu comprimento de onda é totalmente certo e uma vez que uma onda tem uma extensão espacial infinita a sua posição é totalmente incerta.

Vemos que existe uma relação de proporcionalidade inversa entre a dispersão de uma partícula relativamente à sua posição e a dispersão de uma partícula relativamente ao seu comprimento de onda.

Fisicamente a quantidade de interesse é o momento linear e o seguinte resultado é válido:

que é a relação de incerteza de Heisenberg. é a dispersão relativamente à posição da partícula e é a dispersão relativamente ao momento linear da partícula.

É também possível provar com toda a generalidade que para a o tempo necessário para a transição de energia e para a energia transferida vale uma desigualdade análoga.

— 7. Aplicações da Equação de Schroedinger —

Neste capítulo vamos dar uso ao Axioma 10. Este axioma indica como varia um estado quântico ao longo do tempo e é vital para que possamos compreender a dinâmica a nível atómico.

De notar que o Axioma 10 é uma equação diferencial e como tal a teoria assim construída é determinista.

De acordo com o Axioma 11 A probabilidade de encontrar uma partícula no elemento de espaço é . Assim sendo a probabilidade encontrar a partícula num intervalo é .

Uma vez que a equação do Axioma 10 é uma equação linear sabemos que se é solução da equação de Schroedinger também é uma solução da equação de Schroedinger.

Por outro lado temos que ter necessariamente

Deste modo a constante complexa fica fixada a menos de um factor de fase. Uma vez que este factor de fase é irrelevante no contexto deste curso a condição 46 efectivamente faz com que a nossa solução de Schroedinger tenha uma solução única.

De modo a simplificar a nossa discussão vamos supor que . Deste modo em vez da equação que é equação à derivadas parciais temos:

Que são duas equações diferenciais ordinárias.

Da primeira equação vem que a dependência temporal da função de onda é . A segunda equação é conhecida como a equação de Schroedinger independente do tempo e é sobre ela que nos vamos debruçar nas secções seguintes.

— 7.1. Poço de Potencial Infinito —

Apesar de esta situação ser bastante artificial a nível físico a sua componente didáctica é bastante elevada e convém ser estudado de modo a que possamos entender exemplos que tenha alguma relevância física.

Nesta situação a partícula desloca-se ao longo de um comprimento onde não sofre a influência de nenhuma energia potencial. Mas ao chegar as extremidades do comprimento temos . Que é um potencial infinitamente repulsivo.

Para ou é obviamente .

Dentro da região onde o movimento é permitido temos . Solução que nos diz que os valores de energia que a partícula pode ter não mais fazem parte de um intervalo contínuo mas que passam a ser valores discretos.

— 7.2. Poço de Potencial Finito —

Uma situação mais realista é dizermos que uma partícula se desloca ao longo de uma região onde não está sujeita a nenhuma energia potencial e que nas extremidades desta região encontra um potencial . Um potencial que é repulsivo mas finito.

Se assumirmos que ou seja que a energia da partícula é inferior à energia potencial repulsiva vemos que as soluções de 7 permitem uma probabilidade não nula de encontrar a partícula fora da região onde estava inicialmente confinada.

— 7.3. Oscilador Harmónico —

Para oscilações pequenas em torno de um ponto de equilíbrio sabemos que qualquer função de energia potencial pode ser aproximada por uma função quadrática. Assim a dinâmica resultante para partículas que tenham pequenos deslocamentos em torno de uma posição de equilíbrio é em primeira aproximação a dinâmica de um movimento harmónico.

Para o oscilador harmónico a equação de Schroedinger é

Não iremos resolver esta equação de forma exacta mas por argumentos heurísticos vamos propor uma solução possível para o estado fundamental.

Pelos exemplos anteriores vimos que no estado fundamental a função de onda nunca tomava o valor 0 mas aproximava-se dele assintoticamente. Vimos também que as soluções por nós encontradas reflectiam a simetria da energia potencial.

Assim sendo esperamos que o mesmo aconteça neste caso. Uma possível solução será então uma função da forma

Substituindo esta função na equação de Schroedinger vemos que e que . O que mostra que a energia de um oscilador harmónico quântico no estado fundamental não é zero.

É possível demonstrar que

— Bibliografia —

• Physics for Scientists and Engineers 6th Edition R. A. Serway, J. W. Jewett
• Modern Physics 3rd Edition R. A. Serway, C. J. Moses, C. A. Moyer
• The Evolution of Physics A. Einstein, L. Infeld
• Física Atómica 4ª edição Max Born
• The Feynman Lectures on Physics Feynman, Leighton , Sands

— 3. Oscilações e Ondas —

Neste capítulo vamos introduzir algumas noções relacionadas com o movimento ondulatório em geral. Vamos também ver dois fenómenos que no contexto da mecânica clássica só podem ser explicados recorrendo ao conceito de onda.
As ondas e as oscilações são casos particulares de movimento oscilatório e como tal há conceitos básicos que são comuns aos dois tipo de fenómenos:

Definição 18 Período é o intervalo de tempo mínimo necessário para que dois pontos de um mesmo fenómeno ondulatório estejam no mesmo estado físico. O período representa-se pelo símbolo .

Definição 19 Frequência é o número de ciclos de um fenómeno ondulatório que ocorre durante um segundo. Representa-se pela letra e calcula-se utilizando a seguinte expressão .

Definição 20 A frequência angular é

— 3.1. Oscilações —

Nesta secção vamos apenas estudar o movimento harmónico. Este é um tipo de movimento importante uma vez que em primeira aproximação muitos tipos de movimentos oscilatório podem ser aproximados pelo movimento harmónico.

Imaginemos que temos uma partícula que se desloca ao longo de uma posição de equilíbrio e está sujeita a uma força .

Definição 21 Um movimento diz-se harmónico quando num movimento oscilatório a força é proporcional ao deslocamento relativo à posição de equilíbrio e tem o sentido oposto ao do deslocamento.

Recorrendo ao Axioma 2 e introduzindo podemos escrever a equação que descreve o movimento harmónico como

As equações desta solução podem ser da forma em que é o deslocamento máximo relativamente à posição de equilíbrio e é a fase que especifica qual a posição inicial da partícula.

No caso do movimento harmónico as definições 18 e 19 podem ser escritas na forma e .

Para um movimento oscilatório a energia cinética e potencial são:

• 
• 

Assim sendo a energia total do sistema é

— 3.2. Ondas —

Definição 22 Uma onda é uma perturbação que se propaga transportando energia.

Definição 23 Comprimento de onda, , é a distância mínima entre dois pontos da onda que se encontrem nas mesmas condições.

Definição 24 A velocidade uma onda com comprimento de onda e período é

Definição 25 O número de onda é

É possível demonstrar que a equação que representa a propagação de uma perturbação que se move com velocidade constante é:

Com as definições anteriores é imediato ver que equações da forma e são soluções de 14. Estas funções chamam-se sinusoidais, é a amplitude e representa o deslocamento máximo, relativamente à posição de equilíbrio, da entidade que está a vibrar.

Em geral podemos dizer que uma onda progressiva que se propaga para a direita é sempre da forma enquanto que uma onda que se propague para a esquerda é sempre da forma , onde e são funções a especificar.

Uma vez que a equação de onda é linear sabemos que qualquer combinação linear soluções da equação 14 é ainda uma solução da equação 14.

Para que as soluções tenham sentido físico devemos impor certas condições que as equações devem obedecer em determinadas regiões do espaço. Estas condições chamam-se condições de fronteira e o seu efeito é restringir o conjunto de valores que as soluções podem tomar.

As soluções de onda que respeitam as condições fronteira têm o nome de modos normais de vibração.

Quando uma onda se propaga e encontra a fronteira entre dois meios diferentes dois acontecimentos podem ocorrer:

1. Transmissão: alguma da energia da onda propaga-se no segundo meio.
   

   Transmissão de um Pulso de Onda

2. Reflexão: toda a energia da onda se propaga no primeiro meio mas com o sentido oposto.
   

   Reflexão de um Pulso de Onda

Quando duas ondas sinusoidais da mesma amplitude e frequência que se propagam em sentidos opostos geram uma onda resultante cuja equação é dada por . Esta é a equação de uma onda estacionária.

— 3.3. Interferência —

Quando duas ondas do mesmo comprimento de onda e diferença de fase constante se encontram dá-se o fenómeno de interferência .

Se as duas ondas se encontrarem na mesma região do espaço e tiverem a mesma fase a interferência diz-se construtiva e a amplitude do onda resultante é igual à soma das amplitudes de cada onda original.

Se as duas se encontram na mesma região do espaço em oposição de fase a interferência diz-se destrutiva e a amplitude da onda resultante é igual à subtracção da amplitude das duas ondas originais.

A figura seguinte mostra uma representação esquemática de uma realização experimental para se observar um padrão de interferências:

— 3.4. Difracção —

Quando luz de comprimento de onda bem definido incide numa barreira com uma abertura acontece um fenómeno chamado difracção . Cada porção da fenda age como se fosse uma fonte independente e ondas provenientes de porções diferentes têm fases diferentes. Da sua interacção pode resultar interferência construtiva ou interferência destrutiva.

A figura seguinte mostra uma representação esquemática de uma realização experimental para se observar o fenómeno de difracção:

— 4. Electromagnetismo —

A teoria do Electromagnetismo é a primeira teoria Física a ter uma natureza moderna. É uma teoria de campo e para além do mais é uma teoria relativista.

— 4.1. Conceitos Básicos e Definições Preliminares —

Para criar uma teoria electromagnética devemos primeiro introduzir uma nova grandeza fundamental. Essa grandeza é a carga eléctrica que se representa pelo símbolo e a sua unidade no sistema internacional é o coulomb cujo símbolo é .

Definição 26 Campo eléctrico é um campo vectorial, denotado pelo símbolo , criado por uma carga eléctrica (carga fonte).

Definição 27 Um campo eléctrico estabelece entre dois pontos e uma diferença de potencial

Definição 28 A força eléctrica surge da interacção de uma partícula de carga (carga de teste) com o campo eléctrico criado por uma partícula de carga .

Definição 29 Uma carga eléctrica que se desloque de para num campo eléctrico faz com que a energia potencial do sistema varie da seguinte forma

Definição 30 Um campo eléctrico ao passar por uma superfície de forma arbitrária estabelece um fluxo eléctrico que é dado peça seguinte expressão onde representa o vector de norma , direcção perpendicular à superfície.

Definição 31 Corrente eléctrica é a taxa de fluxo de carga eléctrica por unidade de tempo. Se consideramos o seu valor médio é . Se consideramos o seu valor instantâneo é

Definição 32 Campo magnético é um campo vectorial, denotado pelo símbolo , criado por uma carga eléctrica em movimento.

Definição 33 A força magnética surge da interacção de uma partícula de carga com o campo magnético criado por uma partícula de carga .

Definição 34 Um campo magnético ao passar por uma superfície de forma arbitrária estabelece um fluxo magnético que é dado peça seguinte expressão onde representa o vector de norma e direcção perpendicular à superfície .

— 4.2. Axiomas de Maxwell —

No interesse da consistência as equações de Maxwell serão denominadas por axiomas de Maxwell uma vez que o seu papel na teoria do electromagnetismo poder ser considerado equivalente ao papel de axiomas.

Apenas apresentaremos estes axiomas na sua forma integral ainda que estas equações possam ser expressas de modo totalmente equivalente por equações diferenciais.

Axioma 4

Axioma 5

Axioma 6

Axioma 7

O primeiro axioma diz-nos o fluxo eléctrico que passa por uma superfície fechada é proporcional à carga contida no interior da superfície. O segundo axioma é equivalente à afirmação de que não existem cargas magnéticas.

O terceiro axioma expressa o facto que campos magnéticos que variam no tempo criam campos eléctricos. Por sua vez estes campos eléctricos não conservativos são responsáveis por criarem uma diferença de potencial ao longo de um circuito eléctrico.

O quarto axioma expressa o facto que campos eléctricos que variam no tempo e correntes eléctricas criam campos magnéticos. O termo é denominado de corrente de deslocamento.

— 4.2.1. Consequências dos Axiomas de Maxwell —

Recorrendo ao axioma 4 e ao conceito de superfície Gaussiana podemos determinar a a expressão matemática do campo eléctrico de algumas distribuições de carga.

Uma superfície gaussiana tem que ter alguns dos seguintes atributos para permitir o cálculo de :

• O valor do campo eléctrico deve ser constante na superfície.
• A seguinte simplificação deve ser possível .
• .
• O valor do campo eléctrico é 0 na superfície.

Para o caso de uma carga pontual isolada a superfície gaussiana em questão é uma superfície esférica centrada na carga. Neste caso conseguimos obter os dois primeiros atributos e vem:

Se definirmos vem que o potencial eléctrico de uma carga pontual é:

E deste modo a energia de interacção entre uma carga e uma carga separadas de uma distância é:

Para um campo eléctrico uniforme vem que a diferença de potencial entre dois pontos separados de uma distância é

Outras consequências dos axiomas de Maxwell serão exploradas nas series de exercícios.

— 4.3. Ondas Electromagnéticas —

Os axiomas 6 e 6 permitem deduzir que

Se identificarmos vemos que as equações 26 e 27 são equações de onda progressivas que se deslocam com a velocidade .

É um facto experimental que a velocidade de propagação de luz tem um valor muito próximo de e assim surge como hipótese o facto da luz nada mais ser do que um tipo de radiação electromagnética.

Esta hipótese foi posteriormente confirmada experimentalmente por Hertz e é um dos mais espectaculares sucessos da teoria electromagnética.

Outro facto interessante que provém da teoria electromagnética é que é invariante. Isto é uma directa contradição ao que tínhamos visto anteriormente no contexto da Mecânica Clássica (secção 2).

— 5. Teoria da Relatividade Restrita —

Neste momento temos uma codificação bastante boa e consistente de um vasto conjunto de dados experimentais. No entanto temos duas situações algo espinhosas entre as nossas mãos. Em primeiro lugar as transformações de Galileu apenas afirmam a invariância das leis da mecânica. Em segundo lugar temos que a teoria electromagnética prevê que a velocidade da luz não depende do referencial inercial.

A resolução destes problemas no início do século XX acarretou uma profunda revisão dos conceitos de espaço e tempo e os conceitos de massa, energia e inércia.

— 5.1. Conceitos Básicos e Definições Preliminares —

Definição 35 Espaço-tempo é um espaço com três dimensões espaciais e uma dimensão temporal.

Definição 36 Um acontecimento é um ponto no espaço tempo.

Quer isto dizer que de agora em diante deixaremos de pensar no tempo como um parâmetro e que o nosso ênfase na especificação do estado de uma partícula passará para a posição que ela ocupa no espaço-tempo em vez de se focar no seu estado mecânico.

— 5.2. Axiomas de Einstein —

Axioma 8 As leis da Física têm a mesma forma em todos os referenciais inerciais.

Axioma 9 As ondas electromagnéticas têm a mesma velocidade em todos os referenciais inerciais.

O primeiro axioma é uma generalização do que se chama de Princípio de Galileu e o segundo axioma apenas é o constatar de um facto experimental. À primeira vista estes dois axiomas parecem ser incoerentes, mas tal é apenas fruto dos nossos preconceitos relativamente à natureza do espaço e do tempo.

— 5.3. Transformações de Lorentz —

Imaginemos um mesmo acontecimento que é descrito em dois referenciais inerciais diferentes e . Vamos supor que se move relativamente a com uma velocidade constante e que as origens dos dois referenciais coincidem para .

É agora nossa tarefa deduzir as equações que permitam transformar as coordenadas de um referencial para as coordenadas de outro.

Primeiro que tudo vamos notar que devido ao axioma 8 podemos escrever e .

Talvez seja conveniente realçar o facto de termos escrito na segunda equação e que isto quer dizer que a natureza do tempo não é assumida mas sim deduzida.

Após alguma manipulações algébricas obtemos

Ou seja as nossas transformações, denominadas por transformações de Lorentz são

— 5.4. Consequências das Transformações de Lorentz —

As transformações cuja forma acabamos de deduzir têm consequências que parecem verdadeiramente incríveis ao senso comum:

• O espaço e o tempo não mais são entidades absolutas.
• O conceito de acontecimentos simultâneos é relativo ao referencial.
• O comprimento de corpos em movimento encurta na direcção do seu movimento.
• A fórmula para a adição de velocidades tem que ser revista.
• Os conceitos de massa, energia e inércia devem ser repensados.

Entender o porquê da primeira consequência é trivial tendo em conta a forma das transformações de Lorentz. A segunda, terceira e quarta consequências serão demonstradas como exercícios e a última consequência será estudada na secção 5.

— 5.5. Relação entre Massa e Energia —

De modo a obtermos a conservação do momento linear utilizando as transformações de Lorentz a definição de momento linear (definição 14) deve ser revista.

Definição 37 O momento linear de uma partícula que se desloca com velocidade é

Definição 38 Quando o momento linear de uma partícula varia dizemos que a partículas está a ser actuada por uma força

A revisão dos conceitos de momento linear e força no contexto da teoria da relatividade implicam necessariamente a revisão do conceitos de energia cinética e do conceito de inércia.

Sabemos que uma força realiza trabalho sobre uma partícula ao longo de um determinado deslocamento.

Se a força actua na partícula estando esta primeiramente em repouso é

Uma vez que é a energia associada a uma partícula quando esta está em repouso tem que ser a soma da sua energia cinética com a energia em repouso.

Definição 39 A energia total de uma partícula é dada pela equação

Com a definição normal de trabalho e a definição relativista de força concluímos que a energia de uma partícula está relacionada com a sua massa. Quando (partícula em repouso) temos .

Uma vez que na física moderna o conceito de momento linear tem sentido físico enquanto que o conceito de velocidade não, é costume escrever a equação 32 na forma

Esta última equação indica que a massa e a energia são apenas duas faces de uma mesma moeda e que se podem converter uma na outra.

Para além disso também demonstra que a inércia, no contexto relativista, deixa de ser vista como uma medida da massa da partícula e passa a ser vista como uma medida da massa e do momento linear da partícula.

— Introdução —

O objectivo destes apontamentos é servirem de apoio aos estudantes do Engenharia Informática da Faculdade de Engenharia da Universidade Católica de Angola numa breve introdução aos conceitos de Física Moderna.
Uma vez que neste apontamentos os alunos não encontrarão exercícios resolvidos, para além de alguns simples exemplos, e que nem tudo o que será dito nas aulas constará destes apontamentos (a escassez de diagramas é, talvez, a sua falha mais evidente e os poucos diagramas que se encontram nestas folhas devem-se aos livros que constam da bibliografia) a presença nas aulas é fortemente recomendada.

Como se tal não bastasse, nem tudo que será escrito nestes apontamentos será dito nas aulas, e assim a relação entre os apontamentos e as aulas é de complementaridade.

O objectivo deste curso é introduzir alguns conceitos de Física Moderna de uma forma acessível. Como tal será feita uma breve revisão de alguns conceitos, pressupostos e resultados da mecânica clássica, ainda que utilizando alguma terminologia e conceitos mais modernos, e só depois a Física Relativista e Física Quântica serão introduzidas e estudadas.

Os temas que iremos tratar ao longo deste curso serão (quase) sempre introduzidos da mesma maneira: umas quantas definições de conceitos iniciais, uma exposição dos axiomas que regulam o comportamento das entidades definidas e os resultados que se seguem após o enunciado dos axiomas.

Sei bem que esta não é a maneira corrente de ensinar muitos destes tópicos a um nível introdutório, mas escolhi assim fazê-lo porque tal permite brevidade de exposição dos temas tratados e porque me parece que as teorias assim retratadas são manifestamente mais elegantes.

Espero que o que se ganhe em tempo e elegância não seja compensado por uma correspondente perda em pedagogia.

Aos alunos mais interessados recomenda-se a leitura do livro de A. Einstein e L. Infeld A Evolução da Física.

— Desiderata —

Apesar de ao longo do nosso curso nós praticamente não considerarmos experiências, a Física é, acima de tudo, uma ciência exacta e experimental. Assim sendo o seu objectivo deve ser a codificação de um conjuntos de dados experimentais por meio de modelos que permitam uma interpretação dos fenómenos que se decide estudar.

Um facto extraordinário é que a partir da codificação e interpretação de um certo conjunto de dados iniciais por parte de um modelo podemos utilizar esse mesmo modelo para prevermos uma nova classe de fenómenos. O confronto destas previsões com resultados experimentais permitirá concluir qual o domínio de validade da teoria construída.

Vamos então codificar os dados experimentais e construir um modelo que nos permita explicar e entender uma parte do mundo que temos à nossa volta.

— 1. Considerações Iniciais —

Podemos dizer sem estarmos muito longe da verdade que a Física fundamental moderna tem na sua essência três concepções fundamentais:

1. O conceito de campo.
2. A Relatividade.
3. A Física Quântica

O conceito de campo é comum à praticamente todo o nosso curso por isso vamos já defino-lo:

Definição 1 Campo é um objecto matemático que tem um valor definido num dado conjunto de pontos do espaço.

Definição 2 Um campo diz-se vectorial quando os seus valores são grandezas vectoriais.

Definição 3 Um campo diz-se escalar quando os seus valores são grandezas escalares. As equações de campo que vamos descrever representam sempre interacções lineares. Assim podemos considerar cada interacção proveniente de um campo como sendo independente das outras interacções e a resultante é simplesmente a soma de todas as interacções.

Associada ao conceito de campo temos o conceito de energia potencial . Esta energia deve-se à interacção da partícula com o campo e em geral é proporcional a onde é o vector deslocamento infinitesimal.

— 2. Mecânica —

A Mecânica Newtoniana é a primeira teoria Física que vamos estudar. Surgiu no século XVII, ganhou maturidade nos séculos XVIII e XIX e rejuvenesceu no século XX.

Este primeiro capítulo será uma introdução muito breve e superficial dos seus triunfos e resultados, mas ainda assim espero demonstrar alguma da sua extrema elegância e profundidade.

— 2.1. Conceitos Básicos e Definições Preliminares —

Todas as grandezas mecânicas podem ser expressas em unidades que derivam das unidades das três grandezas seguintes:

• Comprimento que se representa pela letra .
• Tempo que se representa pela letra .
• Massa que se representa pela letra . Na mecânica clássica a massa de um corpo é uma indicação da sua resistência a alterar o seu estado de movimento. Esta característica tem o nome de inércia .

As unidades que utilizámos para expressar estas grandezas não têm nada de essencial e são puramente convencionais. Neste curso iremos utilizar o sistema internacional e vem que , e .

Definição 4 Um referencial é um conjunto de eixos que permitem representar os graus de liberdade do sistema em estudo e um ponto arbitrário que serve como origem.

Definição 5 Um referencial diz-se inercial : quando possui as seguintes propriedades: Espaço é homogéneo (todos os pontos são equivalentes) e isotrópico (não existem direcções privilegiadas). Tempo é homogéneo (todos os instantes de tempo são equivalentes).

Definição 6 Posição é o lugar geométrico que a partícula ocupa num dado instante de tempo num referencial.

Definição 7 Trajectória é o lugar geométrico das sucessivas posições que a partícula ocupa num intervalo de tempo.

Definição 8 Deslocamento é a diferença entre a posição final e a posição inicial de uma partícula. Normalmente representamos o deslocamento através do símbolo .

Sabemos pela experiência que os corpos se deslocam percorrendo deslocamentos diferentes em intervalos de tempo diferentes. O conceito que relaciona a variação da posição de uma partícula com o intervalo de tempo necessário para essa variação ocorrer é chamado de velocidade . Mas em física convém sermos mais rigorosos e definirmos dois tipos diferentes de velocidade.

Definição 9 Velocidade média : grandeza vectorial que permite calcular a taxa de variação da posição para um dado intervalo de tempo.

Definição 10 Velocidade instantânea : grandeza vectorial que permite calcular a variação da posição para um dado instante de tempo.

Uma vez que a velocidade das partículas também varia, fenómeno que recebe o nome de aceleração }, podemos introduzir as seguintes definições:

Definição 11 Aceleração média : grandeza vectorial que permite calcular a taxa de variação da velocidade para um dado intervalo de tempo.

Definição 12 Aceleração instantânea : grandeza vectorial que permite calcular a variação da velocidade para um dado instante de tempo.

Convém ainda dizer que normalmente diz-se apenas velocidade (aceleração) em vez de velocidade instantânea (aceleração instantânea).

Associado ao conceito de velocidade temos dois conceitos físicos. Um deles escalar, e portanto fornece menos informação sobre o movimento da partícula, e o outro vectorial.

Definição 13 Energia cinética : energia associada ao movimento de uma partícula e defini-se como sendo:

Definição 14 Momento linear : grandeza vectorial associada ao movimento de uma partícula.

Vemos então o porquê da afirmação da energia cinética conter menos informação sobre o movimento da partícula do que o movimento linear. Pela sua definição a energia cinética não nos dá informação sobre a direcção da velocidade da partícula enquanto que o momento linear nos diz tanto a direcção e a magnitude da velocidade.

Em termos mais prosaicos: o momento linear diz para onde vai a partícula e com que velocidade vai. A energia cinética apenas nos diz com que velocidade vai a partícula.

Definição 15 O estado mecânico de uma partícula é especificado através da determinação simultânea e de precisão infinita das suas coordenadas e do seu momento linear.

— 2.2. Axiomas de Newton —

Até ao momento temos os intervenientes da nossa peça mas ainda não temos as regras que deverão guiar as suas interacções. Estas regras são dadas pelos três axiomas de Newton.

Axioma 1 Existe um referencial inercial onde o momento linear de uma partícula livre mantém sempre o mesmo valor.

Este enunciado não é o que habitualmente se apresenta como a “Primeira Lei de Newton”. Convém então dar uma explicação do porquê da forma deste enunciado.

Anteriormente definimos um referencial inercial, mas a definição que demos é de carácter puramente matemático. Nada neste mundo implica a existência da estrutura matemática que definimos e a função da “Primeira Lei de Newton” é exactamente estipular a existência de um tal referencial no mundo em que habitamos. A justificação desta arrojada hipótese é o espectacular acerto das previsões que a teoria de Newton faz e os resultados obtidos em experiências.

De notar que o habitual enunciado da “Primeira Lei de Newton” está errado em referenciais não inerciais. Uma vez que o habitual enunciado não especifica a que tipo de referencial se refere também ele está, consequentemente, errado.

Outro pormenor interessante é que o Axioma 1 apenas exige a existência de um referencial inercial, mas podemos concluir que existe um número infinito de referenciais inerciais.

Sabemos que num referencial inercial o espaço é homogéneo e isotrópico e que o tempo é homogéneo. Assim sendo o ponto que escolhemos como origem nada tem de especial e podemos efectuar uma translação para um outro ponto qualquer e passar a considerar esse novo ponto como sendo a origem de um novo referencial inercial.

Para além disso podemos rodar todos os nossos eixos em simultâneo e obter novos eixos. Estes novos eixos apenas se distinguem dos antigos por terem novas direcções. Uma vez que o espaço é isotrópico tal facto não acarreta nada de novo e assim este novo referencial continua a ser inercial.

Outra transformação que podemos fazer é obter um referencial que se mova com velocidade constante relativamente ao primeiro referencial. Novamente este situação nada tem de novo e os referenciais continuam a ser equivalentes.

Uma vez que o tempo é homogéneo o instante de tempo que se convencionou ser nada tem de especial. Ou seja um referencial que se obtém de um referencial inercial, alterando o que se considera como sendo o instante inicial, também é um referencial inercial.

Para finalizar temos ainda que dizer que qualquer composição destas transformações também produz um referencial inercial.

Axioma 2 Se o momento linear de uma partícula varia num referencial inercial diz-se que essa partícula foi actuada por uma força, , que se calcula utilizando a seguinte expressão: .

Este axioma reduz-se a quando a massa da partícula é constante. No que se segue iremos sempre considerar que a massa da partícula é constante.

Axioma 3 Quando dois objectos interagem entre si a força (força que o objecto 1 exerce sobre o objecto 2) tem a mesma direcção, é igual em intensidade à força (força que o objecto 2 exerce sobre o objecto 1), mas tem o sentido oposto.

— 2.3. Cinemática e Dinâmica —

Nesta secção vamos introduzir muito esquematicamente considerações que visam descrever e explicar o movimento de uma partícula.

— 2.3.1. Equações de Movimento —

Das definições de aceleração e velocidade que introduzimos na secção 2 resulta o seguinte

Uma vez que a relação funcional da aceleração em função do tempo não é conhecida o lado direito da última igualdade não pode ser calculado.

Temos ainda

Onde também não prosseguimos o cálculo visto que desconhecemos a expressão .

Se consideramos que é constante no tempo (movimento uniformemente acelerado)podemos resolver a equação 2, , e após substituição na equação 8 obtemos

No caso o movimento diz-se rectilíneo uniforme.

— 2.3.2. Transformações de Galileu —

Tínhamos visto após o axioma 1 que existe uma infinidade de referenciais inerciais. Faz então sentido perguntarmo-nos como podemos saber as coordenadas e velocidade de um ponto material num segundo referencial inercial.

Imaginemos que temos dois referenciais e cujas origens coincidem no instante de tempo que convencionámos tomar como origem do tempo. Para além disso move-se com uma velocidade relativamente a .

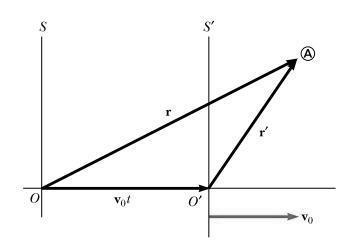
Pela adição de vectores é que podemos escrever na forma de componentes:

Derivando as anteriores equações em ordem ao tempo

As transformações de Galileu são equivalentes à afirmação que a forma das equações da Mecânica não depende do referencial inercial que se escolhe para estudar o movimento.

— 2.3.3. Movimento circular —

Uma vez que a velocidade é uma grandeza vectorial uma partícula diz-se acelerada não só quando a velocidade varia em módulo mas também quando varia em direcção.

Para o movimento ser circular tem que existir uma força que se chama força radial, , que em todos os pontos da trajectória da partícula tem a direcção do centro. Esta força causa uma aceleração radial, também chamada centrípeta, cuja expressão matemática é .

A aceleração responsável pela variação da velocidade em módulo é a aceleração tangencial, .

— 2.4. Campo Gravítico —

A lei da gravitação universal diz que todas as partículas do Universo atraem todas as outras partículas do Universo com uma força que é inversamente proporcional ao quadrado da distância que as separa e directamente proporcional ao produto das suas massas.

Enunciada desta forma esta lei tem o problema de implicar que a interacção gravítica é instantânea. Para solucionarmos este problema vamos apresentar a gravidade como sendo um propriedade emergente de um campo.

Definição 16 Campo Gravítico: Campo vectorial, , criado por um corpo de massa em todos os pontos do espaço (excepto no ponto onde se encontra) que é responsável pela interacção gravítica.

Quando uma partícula de massa é colocada num ponto do espaço onde existe um campo gravítico a partícula interage com este campo gravítico. Ao interagir com o campo gravítico a partícula de massa fica sob a acção de uma força cuja expressão matemática é

Onde é um vector unitário com a direcção da recta que une as duas partículas e com sentido a apontar para .

Para o caso particular de um corpo de massa que esta a metros da superfície da Terra sujeito à sua atracção gravitacional é

Recordando que para corpos de massa constante podemos escrever que a intensidade da aceleração da gravidade é

.

Definição 17 Quando dois corpos de massa e massa interagem graviticamente estabelece-se entre eles uma energia derivada do campo gravítico. Esta energia tem o nome de energia potencial gravítica e a sua expressão matemática é