Início » 04 Ensino Superior » 02 Física » 19 Cálculo IV

Category Archives: 19 Cálculo IV

Equações diferenciais homogéneas.Exercícios resolvidos

03/02/2016 11:48 am / 1 comentário em Equações diferenciais homogéneas.Exercícios resolvidos

— 2. Equações diferenciais homogéneas.Exercícios resolvidos —

No artigo passado apresentamos exercícios resolvidos sobre equações diferenciais com variáveis separáveis, neste artigo vamos tratar de resolver exercícios relacionados a equações diferenciais homogéneas.Aconselhamos ao caro leitor a fazer uma revisão sobre a resolução de integrais.

Exercício 1 Cada uma das equações diferenciais apresentada é homogénea.Resolva as equações diferenciais dadas usando as substituições adequadas.

${(y^{2}+yx)dx+x^{2}dy=0}$
Solução:Usando ${y=ux \Rightarrow dy=udx+xdu}$ , teremos:

$\displaystyle (u^{2}x^{2}+ux^{2})dx+x^{2}(udx+xdu)=0$

dividindo por ${x^{2}}$ temos:

$\displaystyle (u^{2}+u)dx+(udx+xdu)=0 \Rightarrow (u^{2}+2u)dx+xdu)=0$

separando as variáveis,

$\displaystyle \dfrac{dx}{x}+\dfrac{du}{(u^{2}+2u)}$

integrando:

$\displaystyle \ln |x|+\dfrac{1}{2}\ln |u|-\dfrac{1}{2}\ln |u+2|=C$

$\displaystyle 2\ln |x|+\ln |u|-\ln |u+2|=2C$

$\displaystyle \ln\left|\dfrac{x^{2}u}{u+2}\right|=2C \Rightarrow \dfrac{x^{2}u}{u+2}=C_{1}$

como ${u=\dfrac{y}{x}}$ , então:

$\displaystyle \dfrac{x^{2}\dfrac{y}{x}}{\dfrac{y}{x}+2}=C_{1}\Rightarrow x^{2}y=C_{1}(y+2x)$
${\dfrac{dy}{dx}=\dfrac{x+3y}{3x+y}}$
Solução:podemos escrever a equação da seguinte maneira:

$\displaystyle (x+3y)dx-(3x+y)dy=0$

Usando ${y=ux \Rightarrow dy=udx+xdu}$ , teremos:

$\displaystyle (x+3ux )dx-(3x+ux )(udx+xdu)=0$

dividindo por ${x}$ temos:

$\displaystyle (1+3u )dx-(3+u)(udx+xdu)=0$

multiplicando as variáveis e organizando temos

$\displaystyle (u^{2}-1)dx+x(u+3)du=0$

separando as variáveis,

$\displaystyle \dfrac{dx}{x}+\dfrac{u+3}{(u-1)(u+1)}du=0$

integrando

$\displaystyle \ln|x|+2\ln|u-1|-\ln|u+1|=C \Rightarrow \ln\left|\dfrac{x(u-1)^{2}}{u+1}\right|=C$

$\displaystyle \dfrac{x(u-1)^{2}}{u+1}=C_{1}$

sabemos que ${u=\dfrac{y}{x}}$ , então:

$\displaystyle \dfrac{x\left(\dfrac{y}{x}-1\right)^{2}}{\dfrac{y}{x}+1}=C_{1}\Rightarrow (y-x)^{2}=C_{1}(y+x)^{2}$
${xdx+(y-2x)dy=0}$
Solução:Usando ${x=vy \Rightarrow dx=vdy+ydv}$ , teremos:

$\displaystyle vy(vdy+ydv)+(y-2vy)dy=0$

dividindo por ${y}$ temos:

$\displaystyle v(vdy+ydv)+(1-2v)dy=0$

multiplicando as variáveis e organizando temos:

$\displaystyle vydv+(v^{2}-2v+1)dy=0$

separando as variáveis temos

$\displaystyle \dfrac{vdv}{(v-1)^{2}}+\dfrac{dy}{y}=0\Rightarrow \dfrac{(v-1)dv}{(v-1)^{2}}+\dfrac{dv}{(v-1)^{2}}+\dfrac{dy}{y}=0$

integrando

$\displaystyle \ln |v-1|-\dfrac{1}{v-1}+\ln |y|=C$

sabemos que ${v=\dfrac{x}{y}}$ então:

$\displaystyle \ln \left|\dfrac{x}{y}-1\right|-\dfrac{1}{\dfrac{x}{y}-1}+\ln |y|=C$

podemos escrever a solução da seguinte maneira

$\displaystyle (x-y)\ln |x-y|-y=C(x-y)$
${[x-y\arctan (y/x)]dx+x\arctan (y/x)dy=0}$
Solução:se ${y=ux \Rightarrow dy=udx+xdu}$ , substituindo na equação temos:

$\displaystyle [x-ux\arctan u]dx+x\arctan u(udx+xdu)=0$

simplificando as variáveis temos:

$\displaystyle dx+x\arctan u du=0$

separando as variáveis tem-se

$\displaystyle \dfrac{dx}{x}+\arctan udu=0$

integrando,

$\displaystyle \ln|x|+u\arctan u-\dfrac{1}{2}\ln |1+u^{2}|=\ln C$

como ${u=\dfrac{y}{x}}$ , então:

$\displaystyle \ln|x|+\dfrac{y}{x}\arctan \left(\dfrac{y}{x}\right)-\dfrac{1}{2}\ln \left|1+\left(\dfrac{y}{x}\right)^{2}\right|=\ln C$

organizando a solução tem-se:

$\displaystyle 2y\arctan \left(\dfrac{y}{x}\right)=x\ln \left|\dfrac{x^{2}+y^{2}}{x^{4}}\right|+C_{1}$

onde ${C_{1}=\ln C^{2}}$
${[y\cos (y/x)+x\sin (y/x)]dx=x\cos (y/x)dy}$
Solução:se ${y=ux \Rightarrow dy=udx+xdu}$ , substituindo na equação dada obtemos:

$\displaystyle (ux\cos u+x\sin u)dx=x\cos u (udx+xdu)$

agrupando os termos semelhantes e simplificando obtém-se:

$\displaystyle \sin udx=x\cos udu$

separando as variáveis,

$\displaystyle \dfrac{dx}{x}=\dfrac{\sin u}{\cos u}du$

integrando,

$\displaystyle \ln x=\ln \sin u +\ln C\Rightarrow x=C\sin u$

como ${u=\dfrac{y}{x}}$ , então:

$\displaystyle x=C\sin \dfrac{y}{x}$
${x\dfrac{dy}{dx}=y+\sqrt{x^{2}+y^{2}}}$
Solução:A equação diferencial dada pode ser escrita da seguinte maneira:

$\displaystyle (y+\sqrt{x^{2}+y^{2}})dx-xdy=0$

se ${y=ux \Rightarrow dy=udx+xdu}$ , substituindo na equação acima obtemos:

$\displaystyle (ux+\sqrt{x^{2}+u^{2}x^{2}})dx-x(udx+xdu)=0$

agrupando os termos e simplificando temos:

$\displaystyle x\sqrt{1+u^{2}}dx-x^{2}du=0$

separando as variáveis:

$\displaystyle \dfrac{dx}{x}-\dfrac{du}{\sqrt{1+u^{2}}}=0$

integrando,

$\displaystyle \ln |x|-\ln \left|u+\sqrt{1+u^{2}}\right|= C \Rightarrow \dfrac{x}{(u+\sqrt{1+u^{2}})}=e^{C}$

como ${u=\dfrac{y}{x}}$ , então:

$\displaystyle \dfrac{x}{\dfrac{y}{x}+\sqrt{1+\left(\dfrac{y}{x}\right)^{2}}}=C_{1}$

simplificando a equação temos

$\displaystyle x^{2}=C_{1}(y+\sqrt{y^{2}+x^{2}})$

Exercício 2 Resolva os problemas com os valores iniciais dados usando substituições apropriadas

${ydx+x(\ln x-\ln y-1)dy=o, \quad y(1)=e}$
Solução:Se ${x=vy \Rightarrow dx=vdy+ydv}$ substituirmos na equação, teremos:

$\displaystyle y(vdy+ydv)+vy(\ln vy-\ln y-1)dy=o$

$\displaystyle (vdy+ydv)+v(\ln v+ \ln y-\ln y-1)dy=o$

$\displaystyle vdy+ydv+v\ln v dy-vdy=o\Rightarrow ydv+v\ln v dy=0$

separando as variáveis:

$\displaystyle \dfrac{dv}{v\ln v}+\dfrac{dy}{y}=0$

integrando

$\displaystyle \ln|\ln |v||+\ln |y|=C \Rightarrow \ln |y\ln |v||=C\Rightarrow y\ln |v|=C_{1}$

sabemos que ${v=\dfrac{x}{y}}$ então:

$\displaystyle y\ln \left|\dfrac{x}{y}\right|=C_{1}$

usando ${y(1)=e}$ nos encontramos

$\displaystyle e\ln \left|\dfrac{1}{e}\right|=C_{1}\Rightarrow C_{1}=-e$

a solução do problema de valor inicial será:

$\displaystyle y\ln \left|\dfrac{x}{y}\right|=-e$
${(x+ye^{y/x})dx-xe^{y/x}dy=0, \quad y(1)=0}$
Solução:Usando ${y=ux \Rightarrow dy=udx+xdu}$ , teremos:

$\displaystyle (x+uxe^{u})dx-xe^{u}(udx+xdu)=0$

dividindo por ${x}$ temos:

$\displaystyle (1+ue^{u})dx-e^{u}(udx+xdu)=0$

multiplicando e organizando as variáveis teremos:

$\displaystyle dx-xe^{u})du=0$

agora vamos separar as variáveis

$\displaystyle \dfrac{dx}{x}-e^{u}du=0$

integrando a equação temos

$\displaystyle \ln |x|-e^{u}=C$

sabemos que ${u=\dfrac{y}{x}}$ , então:

$\displaystyle \ln |x|-e^{\frac{y}{x}}=C$

usando ${y(1)=0}$ , obtemos

$\displaystyle \ln |1|-e^{\frac{0}{1}}=C \Rightarrow C=-1$

A solução do problema de valor inicial é:

$\displaystyle \ln |x|-e^{u}=-1$
${(x^{2}+2y^{2})dx-xydy=0, \quad y(-1)=1}$
Solução:Usando ${y=ux \Rightarrow dy=udx+xdu}$ , teremos:

$\displaystyle (x^{2}+2u^{2}x^{2})dx-ux^{2}(udx+xdu)=0$

vamos dividir por ${x^{2}}$ e depois multiplicamos e simplificamos os termos semelhantes:

$\displaystyle (1+u^{2})dx-uxdu=0$

separando as variáveis,

$\displaystyle \dfrac{dx}{x}-\dfrac{udu}{1+u^{2}}=0$

integrando,

$\displaystyle \ln |x|-\dfrac{1}{2}\ln |1+u^{2}|=C\Rightarrow \dfrac{x^{2}}{1+u^{2}}=e^{2C}$

como ${u=\dfrac{y}{x}}$ , então:

$\displaystyle \dfrac{x^{2}}{1+\left(\dfrac{y}{x}\right)^{2}}=C_{1}$

organizando a equação,

$\displaystyle x^{4}=C_{1}(y^{2}+x^{2})$

usando a condição inicial ${y(-1)=1}$ temos:

$\displaystyle (-1)^{4}=C_{1}(1^{2}+(-1)^{2})\Rightarrow C_{1}=\dfrac{1}{2}$

A solução do problema de valor inicial é:

$\displaystyle x^{4}=\dfrac{1}{2}(y^{2}+x^{2})$

No próximo artigo vamos apresentar exercícios resolvidos sobre as equações diferenciais exatas.

Equações diferenciais de variáveis separáveis.Exercícios resolvidos

03/01/2016 12:38 am / 3 comentários em Equações diferenciais de variáveis separáveis.Exercícios resolvidos

— 1. Equações diferenciais de variáveis separáveis.Exercícios resolvidos —

Iniciaremos uma serie de artigos com exercícios resolvidos de equações diferenciais.Neste artigo vamos nos concentrar apenas em equações diferenciais de variáveis separáveis o próximo artigo será sobre as equações diferenciais homogéneas.

Exercício 1 Resolver as seguintes equações diferenciais por separação de variáveis

${(xy^{2}-y^{2}+x-1)dx+(x^{2}y-2xy+x^{2}+2y-2x+2)dy=0 }$
Solução:Agrupando, teremos:

$\displaystyle [y^{2}(x-1)+(x-1)]dx+[x^{2}(y+1)-2x(y+1)+2(y+1)]dy=$

$\displaystyle (y^{2}+1)(x-1)dx+(x^{2}-2x+2)(y+1)dy=0$

separando as variáveis teremos

$\displaystyle \dfrac{(x-1)dx}{(x^{2}-2x+2)}+\dfrac{(y+1)dy}{(y^{2}+1)}=0$

integrando

$\displaystyle \int\dfrac{(x-1)dx}{(x^{2}-2x+2)}+\int\dfrac{ydy}{(y^{2}+1)}+\int\dfrac{dy}{(y^{2}+1)}=0$

teremos

$\displaystyle \dfrac{1}{2}\ln (x^{2}-2x+2)+\dfrac{1}{2}\ln (y^{2}+1)+\arctan y=C_{1}$

$\displaystyle \ln [(x^{2}-2x+2)(y^{2}+1)]+2\arctan y=2C_{1}$

$\displaystyle \ln [(x^{2}-2x+2)(y^{2}+1)]=2C_{1}-2\arctan y$

levantando o logaritmo e fazendo ${C_{2}=e^{2C_{1}}}$ teremos

$\displaystyle [(x^{2}-2x+2)(y^{2}+1)]=C_{2}e^{-2\arctan y}$

onde se tem:

$\displaystyle [(x^{2}-2x+2)(y^{2}+1)]e^{2\arctan y}=C_{2}$
${\sin 3xdx +2y\cos^{3}3xdy=0 }$
Solução:separando as variáveis teremos

$\displaystyle 2ydy=-\dfrac{\sin 3x}{\cos^{3}3x}dx \Rightarrow 2ydy=-\left(\dfrac{\sin3x}{\cos3x}\right)\left(\dfrac{1}{\cos^{2}3x}\right)$

$\displaystyle 2ydy=-\tan3x\sec^{2}3xdx$

integrando obtemos:

$\displaystyle \int2ydy=-\dfrac{1}{6}\int d(\sec^{2}3x)$

$\displaystyle y^{2}=-\dfrac{1}{6}\sec^{2}3x+c$
${e^{x}y\dfrac{dy}{dx}=e^{-y}+e^{-2x-y}}$
Solução:organizando a equação e separando as variáveis temos:

$\displaystyle e^{x}y\dfrac{dy}{dx}=e^{-y}(1+e^{-2x})\Rightarrow ye^{y}dy=\dfrac{1+e^{-2x}}{e^{x}}dx$

integrando obtemos:

$\displaystyle \int ye^{y}dy=\int (e^{-x}+e^{-3x})dx$

a integral do lado esquerdo resolve-se aplicando integração por partes.

$\displaystyle \int udv=uv-\int vdu$

Supondo que

$\displaystyle u=y \Rightarrow du=dy; \quad dv=e^{y}dy \Rightarrow v=e^{y}$

teremos:

$\displaystyle \int ye^{y}dy=ye^{y}-\int e^{y}dy=ye^{y}-e^{y}$

tendo a integral do lado esquerdo e do lado direito resolvida agora sim podemos dizer que a solução da equação diferencial será:

$\displaystyle ye^{y}-e^{y}=-e^{-x}-\dfrac{1}{3}e^{-3x}+C \Rightarrow ye^{y}-e^{y}+e^{-x}+\dfrac{1}{3}e^{-3x}=C$

Exercício 2 Ache a solução da equação diferencial que satisfaça a condição inicial dada.

${(1+x^{4})dy+x(1+4y^{2})dx=0, \quad y(1)=0}$
Solução:separando as variáveis temos:

$\displaystyle \dfrac{dy}{1+4y^{2}}+ \dfrac{xdx}{1+x^{4}}=0\Rightarrow \int \dfrac{dy}{1+(2y)^{2}}+\int \dfrac{xdx}{1+(x^{2})^{2}}=0$

$\displaystyle \dfrac{1}{2}\arctan 2y+\dfrac{1}{2}\arctan x^{2}=C\Rightarrow \arctan 2y+\arctan x^{2}=C_{1}$

usando ${y(1)=0}$ obtemos ${C_{1}=\frac{\pi}{4}}$ , então:

$\displaystyle \arctan 2y+\arctan x^{2}=\frac{\pi}{4}$
${\dfrac{dy}{dx}+\dfrac{1+y^{3}}{xy^{2}(1+x^{2})}, \quad y(1)=1}$
Solução:Organizando a equação e separando as variáveis teremos:

$\displaystyle xy^{2}(1+x^{2})dy+(1+y^{3})dx=0\Rightarrow \dfrac{y^{2}}{1+y^{3}}dy+\dfrac{1}{x(1+x^{2})}dx=0$

$\displaystyle \dfrac{y^{2}}{1+y^{3}}dy+\dfrac{(1+x^{2})-x^{2}}{x(1+x^{2})}dx=0 \Rightarrow \dfrac{y^{2}}{1+y^{3}}dy +\dfrac{dx}{x}-\dfrac{xdx}{1+x^{2}}=0$

integrando temos:

$\displaystyle \dfrac{1}{3}\ln (1+y^{3})+\ln x -\dfrac{1}{2}\ln(1+x^{2})=C$

$\displaystyle 2\ln (1+y^{3})+6\ln x -3\ln(1+x^{2})=6C$

$\displaystyle \ln \dfrac{x^{6}(1+y^{3})^{2}}{(1+x^{2})^{3}}=6C \Rightarrow \dfrac{x^{6}(1+y^{3})^{2}}{(1+x^{2})^{3}}=e^{6C}$

logo,

$\displaystyle \dfrac{x^{6}(1+y^{3})^{2}}{(1+x^{2})^{3}}=C_{1}$

usando ${y(1)=1}$ , obtemos ${C_{1}=\frac{1}{2}}$ e a solução será:

$\displaystyle \dfrac{x^{6}(1+y^{3})^{2}}{(1+x^{2})^{3}}=\dfrac{1}{2}$
${x\cos x=(2y+3e^{3y})y\prime, \quad y(0)=0}$
Solução:

$\displaystyle x\cos x dx=(2y+3e^{3y})dy \Rightarrow \int(2y+3e^{3y})dy=\int x\cos x dx$

a integral do lado esquerdo resolve-se aplicando integração por partes.

$\displaystyle \int udv=uv-\int vdu$

Supondo que

$\displaystyle u=x \Rightarrow du=dx; \quad dv=\cos xdy \Rightarrow v=\sin x$

então,

$\displaystyle \int x\cos x dx=x\sin x-\int \sin x dx=x\sin x+\cos x$

tendo resolvido a integral por partes,agora estamos em condições para apresentar a solução da equação diferencial:

$\displaystyle y^{2}+\dfrac{1}{3}e^{3y}=x\sin x +\cos x +C$

usando ${y(0)=0}$ na equação acima obtemos ${ C=-\dfrac{2}{3}}$ ,nesse caso a solução será:

$\displaystyle y^{2}+\dfrac{1}{3}e^{3y}=x\sin x +\cos x -\dfrac{2}{3}$
${y\prime\tan x= a+y, \quad y(\frac{\pi}{3})=a, \quad 0<x<\frac{\pi}{2}}$
Solução:

$\displaystyle \dfrac{dy}{dx}\dfrac{\sin x}{\cos x}= a+y \Rightarrow \dfrac{dy}{ a+y}=\dfrac{\cos x}{\sin x}dx, \quad [ a+y\neq 0]$

$\displaystyle \int\dfrac{dy}{ a+y}=\int\dfrac{\cos x}{\sin x}dx \Rightarrow \ln (a+y)=\ln (\sin x)+C$

$\displaystyle a+y=e^{\ln (\sin x)+C}=e^{\ln (\sin x)}e^{C}$

aplicando as propriedades de logaritmo e fazendo ${C_{1}=e^{C}}$ temos:

$\displaystyle a+y=C_{1}\sin x$

usando a condição inicial ${y(\frac{\pi}{3})=a}$ obtemos:

$\displaystyle a+a=C_{1}\sin (\frac{\pi}{3}) \Rightarrow 2a=C_{1}\dfrac{\sqrt{3}}{2} \Rightarrow C_{1}=\dfrac{4a}{\sqrt{3}}$

então,

$\displaystyle a+y=\dfrac{4a}{\sqrt{3}}\sin x \Rightarrow y=\dfrac{4a}{\sqrt{3}}\sin x - a$

Exercício 3 Resolva o problema de valor inicial

$\displaystyle y\prime=2x\sqrt{1-y^{2}}, \quad y(0)=0$

e faça um gráfico.

Solução:

$\displaystyle \dfrac{dy}{dx}=2x\sqrt{1-y^{2}} \Rightarrow \dfrac{dy}{\sqrt{1-y^{2}}}=2xdx$

$\displaystyle \int \dfrac{dy}{\sqrt{1-y^{2}}}=\int 2xdx \Rightarrow \arcsin y=x^{2}+C$

usando a condição inicial ${y(0)=0}$ obtemos:

$\displaystyle \arcsin 0=0 + C \Rightarrow C=0$

então:

$\displaystyle \arcsin y=x^{2}\Rightarrow y=\sin (x^{2}), \quad -\sqrt{\pi/2}\leq x\leq \sqrt{\pi/2}$

Figura 1:Gráfico do exemplo 3

Exercício 4 Encontre a solução da equação diferencial

$\displaystyle \dfrac{dy}{dx}=y^{2}-4$

quando se utiliza ${\ln C_{1}}$ como a constante de integração do lado esquerdo da solução e ${4\ln C_{1}}$ substitui-se por ${\ln C}$ .Depois resolve o mesmo problema com o valor inicial ${y(\frac{1}{4})=1}$

Solução:separando as variáveis teremos:

$\displaystyle \dfrac{dy}{y^{2}-4}=dx\Rightarrow \left[\dfrac{\frac{1}{4}}{y-2}-\dfrac{\frac{1}{4}}{y+2}\right]dy=dx$

integrando teremos:

$\displaystyle \dfrac{1}{4}\ln (y-2)-\dfrac{1}{4}\ln (y+2)+\ln C_{1}=x$

substituindo ${4\ln C_{1}}$ por ${\ln C}$ temos:

$\displaystyle \ln (y-2)-\ln (y+2)+\ln C=4x\Rightarrow \ln \left[\dfrac{C(y-2)}{y+2}\right]=4x$

$\displaystyle C\dfrac{y-2}{y+2}=e^{4x} \Rightarrow y=\dfrac{2(C+e^{4x})}{(C-e^{4x})}$

aplicando a condição inicial ${y(\frac{1}{4})=1}$ , obtemos:

$\displaystyle 1=\dfrac{2\left[ C+e^{4(\frac{1}{4})}\right]}{\left[ C-e^{4(\frac{1}{4})}\right]}\Rightarrow 1=\dfrac{2(C+e)}{(C-e)}$

$\displaystyle C-e=2C-2e \Rightarrow C=-3e$

então a solução será:

$\displaystyle y=\dfrac{2(-3e+e^{4x})}{(-3e-e^{4x})}\Rightarrow y=2\dfrac{(3-e^{4x-1})}{(3+e^{4x-1})}$

Aplicação das equações diferenciais de primeira ordem.Misturas

02/28/2016 1:43 pm / Deixe um comentário

— 3.5. Misturas —

Fazer uma mistura é um procedimento extremamente rotineiro em nossas vidas. Com certeza, todos nós já fizemos uma ou várias. Uma mistura é constituída por duas ou mais substâncias, sejam elas simples ou compostas. As proporções entre os constituintes de uma mistura podem ser alterados por processos químicos, como a destilação. Todas as substâncias que compartilham um mesmo sistema, portanto, constituem uma mistura. Não se pode, entretanto, confundir misturar com dissolver. Água e óleo, por exemplo, misturam-se mas não se dissolvem. Isso torna o sistema água ${+}$ óleo uma mistura, não uma solução.

Figura 1:Mistura da água e o óleo

A mistura de dois fluidos algumas vezes dá origem a uma equação diferencial de primeira ordem.Nos problemas de misturas se deseja calcular a quantidade de uma substancia ${Q(t)}$ que há em um recipiente em qualquer instante ${t}$ .

Vamos supor que um tanque contenha uma mistura de água e sal com um volume inicial de ${V_{0}}$ litros e ${Q_{0}}$ gramas de sal e que uma solução salina seja bombeada para dentro do tanque a uma taxa de ${q_{e}}$ litros por minuto possuindo uma concentração de ${C_{e}}$ gramas de sal por litro.Suponha que a solução bem misturada sai a uma taxa de ${q_{s}}$ litros por minuto.

A taxa de variação da quantidade de sal no tanque é igual a taxa com que entra sal no tanque menos a taxa com que sai sal no tanque.

$\displaystyle \dfrac{dQ}{dt}={Taxa \quad de \quad entrada \choose de \quad sal}-{Taxa \quad de \quad saida \choose de \quad sal}$

$\displaystyle \dfrac{dQ}{dt}=R_{e}-R_{s} \ \ \ \ \ (1)$

A taxa com que entra sal no tanque é igual a taxa com que entra a mistura, ${q_{e}}$ , vezes a concentração de entrada, ${C_{e}}$ , ou seja:

$\displaystyle R_{e}=q_{e}\cdot C_{e} \ \ \ \ \ (2)$

E a taxa com que sai sal do tanque é igual a taxa com que sai a mistura do tanque, ${q_{s}}$ , vezes a concentração de sal que sai do tanque, ${C_{s}}$ ,ou seja:

$\displaystyle R_{s}=q_{s}\cdot C_{s} \ \ \ \ \ (3)$

Como a solução é bem misturada a concentração de sal que sai do tanque, ${C_{s}}$ , é igual a concentração de sal no tanque, isto é:

$\displaystyle C_{s}=\dfrac{Q}{V} \ \ \ \ \ (4)$

onde ${V}$ é o volume no tanque.

Como o volume no tanque, ${V}$ , é igual ao volume inicial, ${V_{0}}$ , somado ao volume que entra no tanque menos o volume que sai do tanque, então:

$\displaystyle V=V_{0}+(\vartriangle q)t \ \ \ \ \ (5)$

onde ${\vartriangle q=q_{e}-q_{s}}$

Assim, a quantidade de sal no tanque, ${Q}$ , é a solução do problema de valor inicial

$\displaystyle \left\{\begin{array}{ll} \dfrac{dQ}{dt}=q_{e}C_{e}-q_{s}\dfrac{Q}{V_{0}+(\vartriangle q)t}\\ Q(0)=Q_{0} \end{array}\right. \ \ \ \ \ (6)$

Distingue-se os seguintes casos particulares:

${q_{e}=q_{s}}$ . O volume é constante
${q_{e}>q_{s}}$ . O volume aumenta
${q_{e}<q_{s}}$ . O volume diminui

Figura 2:Tanque com uma mistura

Exemplo 1 Em certo tanque ha ${180}$ litros de solução salina que contem 10Kg de sal.Despeja-se água no tanque com uma velocidade de ${4}$ litros por minuto e sai a mistura com velocidade de ${3}$ litros por minuto .A concentração se mantém homogénea.Achar a quantidade de sal depois de meia hora.

Solução:O exemplo nos fornece os seguintes dados

Volume inicial: ${V_{0}=180l}$
Quantidade de sal: ${Q_{0}=10Kg}$
Velocidade da agua ao entrar: ${q_{e}=4l/min}$
Velocidade da agua ao sair: ${q_{s}=3l/min}$
concentração de sal no inicio: ${C_{e}=0}$ .A água entra sem sal

Se ${Q}$ é a quantidade de sal no tanque em um dado momento.O volume de solução salina em qualquer momento é

$\displaystyle V=V_{0}+(q_{e}-q_{s})t$

a concentração de sal é:

$\displaystyle C=\dfrac{Q}{V}=\dfrac{Q}{V_{0}+(q_{e}-q_{s})t}$

a quantidade de sal no tanque, ${Q(t)}$ , é a solução do problema de valor inicial

$\displaystyle \left\{\begin{array}{ll} \dfrac{dQ}{dt}=-q_{s}\dfrac{Q}{V_{0}+(q_{e}-q_{s})t}\\ Q(0)=Q_{0} \end{array}\right. \ \ \ \ \ (7)$

$\displaystyle \left\{\begin{array}{ll} \dfrac{dQ}{dt}=-3\dfrac{Q}{180+(4-3)t}\\ Q(0)=10 \end{array}\right. \ \ \ \ \ (8)$

A equação ${(8) }$ é linear e pode ser escrita como

$\displaystyle \dfrac{dQ}{dt}+3\dfrac{Q}{180+t}=0 \ \ \ \ \ (9)$

Um fator integrante é neste caso

$\displaystyle \mu (t)=e^{\int \frac{3}{180+t}}dt=e^{3\ln(180+t)}=(180+t)^{3}$

multiplicando a equação ${(9)}$ por ${\mu (t)}$ obtemos:

$\displaystyle (180+t)^{3}\dfrac{dQ}{dt}+3Q(180+t)^{2}=0 \Rightarrow \dfrac{d}{dt}\left[(180+t)^{3}Q\right]=0$

Integrando-se obtemos:

$\displaystyle (180+t)^{3}Q=c$

ou seja,

$\displaystyle Q=\dfrac{c}{(180+t)^{3}}$

substituindo ${t=0}$ e ${Q=10 \Rightarrow c=58\cdot32\times 10^{6}}$

substituindo o valor de ${c}$ encontrado temos:

$\displaystyle Q=\dfrac{58\cdot32\times 10^{6}}{(180+t)^{3}}$

para ${t=30}$ , a quantidade de sal depois de meia hora será:

$\displaystyle Q(30)=6.3 kg$

Exemplo 2 Um tanque com a capacidade de ${400}$ litros contem inicialmente ${200}$ litros de uma mistura de sal e agua (salmoura) com ${30}$ gramas de sal dissolvidos.Despeja-se uma solução com ${1}$ grama de sal por litro a uma taxa de ${4}$ litros por minuto; a mistura se mantém uniforme mediante a agitação e do sal a uma taxa de ${2}$ litros por minuto.Calcule a quantidade de gramas de sal no tanque no momento em que começa a transbordar.

Solução: o exemplo nos fornece os seguintes dados:

Volume no tanque: ${V=400l}$
Volume inicial: ${V_{0}=200l}$
Quantidade de sal dissolvido: ${Q_{0}=30gr}$
Concentração de sal que entra: ${C_{e}=1gr/l}$
Velocidade da solução ao entrar:; ${q_{e}=4l/min}$
Velocidade da mistura ao sair: ${q_{s}=2l/min;}$

o objetivo é achar ${Q(t_{f})}$ onde ${t_{f}}$ é o tempo que o tanque leva para encher.Mas primeiro vamos achar a quantidade de sal (em gramas) ${Q(t)}$ no tanque em qualquer instante ${t}$ antes de transbordar.A taxa de variação ${Q(t)}$ é:

$\displaystyle \dfrac{dQ}{dt}=R_{e}-R_{s} \ \ \ \ \ (10)$

A taxa de entrada ${R_{e}}$ de sal é:

$\displaystyle R_{e}=q_{e}C_{e}=4\cdot 1=4gr/min$

A taxa de saída ${R_{s}}$ de sal é:

$\displaystyle R_{s}=q_{s}C_{s}=2.\dfrac{Q}{V}$

onde ${V}$ é volume do tanque no instante ${t}$ .Como no tanque entra ${4l/min}$ e sai ${2l/min}$ o liquido acumulara no tanque uma taxa de:

$\displaystyle \vartriangle q=q_{e}-q_{s}=4-2=2l/min$

Naturalmente, o tempo que demora a encher o tanque é

$\displaystyle t_{f}=\dfrac{\vartriangle V}{\vartriangle q}=\dfrac{200}{2}=100min$

mas,

$\displaystyle V(t)=V_{0}+(\vartriangle q)t=200+2t=2(100+t)$

substituindo ${V(t)}$ na equação da taxa de saída do sal teremos:

$\displaystyle R_{s}=q_{s}C_{s}=2.\dfrac{Q}{2(100+t)}=\dfrac{Q}{(100+t)}$

ao substituir ${R_{e}}$ e ${R_{s}}$ na equação ${(10)}$ obtemos o seguinte problema de valor inicial

$\displaystyle \dfrac{dQ}{dt}=4-\dfrac{Q}{t+100}; \quad Q(0)=30 \ \ \ \ \ (11)$

a equação ${(11)}$ é uma equação diferencial linear, e pode ser escrita da seguinte forma:

$\displaystyle \dfrac{dQ}{dt}+\dfrac{Q}{t+100}=4$

o fator integrante neste caso será:

$\displaystyle \mu (x)=e^{\int \frac{dt}{t+100}}=e^{\ln (t+100)}\Rightarrow \mu (x)=(t+100)$

multiplicando a equação ${(11)}$ por ${\mu (x)}$ , teremos:

$\displaystyle (t+100)\dfrac{dQ}{dt}+(t+100)=4(t+100)\Rightarrow \dfrac{d}{dt}\left[Q(t+100)\right]=4(t+100)$

Integrando-se obtemos:

$\displaystyle Q(t)=2(t+100)+\dfrac{C}{t+100}$

Aplicando a condição inicial ${Q(0)=30}$ obtemos: ${C=-17000}$ . por tanto a solução ao PVI é:

$\displaystyle Q(t)=2(t+100)-\dfrac{17000}{t+100}$

Para ${t_{f}=100, }$ a quantidade de sal no momento que transborda é

$\displaystyle Q(100)=315gramas$

Aplicação das equações diferenciais de primeira ordem.Corpos em queda

02/24/2016 4:15 pm / 1 comentário em Aplicação das equações diferenciais de primeira ordem.Corpos em queda

— 3.4. Corpos em queda —

Para construir um modelo matemático do movimento de um corpo em um campo de força, em geral iniciamos com a segunda lei do movimento de Newton.Lembre-se da física elementar que a primeira lei do movimento de Newton estabelece que o corpo permanecera em repouso ou continuara movendo-se a uma velocidade constante, a não ser que esteja agindo sobre ele uma força externa.Em cada caso, isso equivale a dizer que quando a soma das forças,isto é, a força resultante, que age sobre sobre o corpo for diferente de zero, essa força resultante será proporcional a aceleração ou mais precisamente:

$\displaystyle F=\sum F_{r}=m\cdot a \ \ \ \ \ (1)$

onde ${m}$ é a massa do corpo.

Suponha agora que uma pedra seja jogada para acima do topo de um prédio, conforme a figura ${1}$ .

Figura 1:Corpos em queda

Qual é a posição ${s(t)}$ da pedra em relação ao chão no instante ${t}$ ?A aceleração da pedra é ${ \frac{d^{2}s}{dt^{2}}}$ .1Se assumirmos como positiva a direção para cima e que nenhuma outra força alem da gravidade age sobre a pedra, obteremos a segunda lei de Newton

$\displaystyle m\frac{d^{2}s}{dt^{2}}=-mg \quad ou \quad \frac{d^{2}s}{dt^{2}}=-g \ \ \ \ \ (2)$

Em outras palavras, a força resultante é simplesmente o peso da pedra próximo a superfície da terra,ou seja:

$\displaystyle F=F_{1}=-P \ \ \ \ \ (3)$

Lembre-se de que a magnitude do peso é ${P=m\cdot g}$ , onde ${g}$ é a aceleração de gravidade.O sinal de subtração foi usado em (2), pois o peso da pedra é uma força dirigida par baixo, oposta a direção positiva.Se a altura do prédio é ${s_{0}}$ e a velocidade inicial da pedra é ${v_{0}}$ , então ${s}$ é determinada, com base no problema de valor inicial de segunda ordem

$\displaystyle \frac{d^{2}s}{dt^{2}}=-g, \quad s(0)=s_{0}, \quad s\prime(0)=v_{0} \ \ \ \ \ (4)$

Embora não estejamos dando enfaze a resolução das equações obtidas, note que a equação ${(4)}$ pode ser resolvida integrando-se a constante ${-g}$ duas vezes em relação a t.As condições iniciais determinam duas constante de integração.Podemos obter a solução de ${(4)}$ como a fórmula

$\displaystyle s(t)=-\dfrac{1}{2}gt^{2}+v_{0}t+s_{0} \ \ \ \ \ (5)$

— 3.4.1. Corpos em queda e a resistência do ar —

Antes dos famosos experimentos de Galileu na torre inclinada de Pisa, acreditava-se que os objetos mais pesados em queda livre, como uma bala de canhão, caiam com uma aceleração maior do que a de objetos mais leves, como uma pena.Obviamente, uma bala de canhão e uma pena , quando largadas simultaneamente da mesma altura, caem a taxas diferentes, mas isso não se deve ao fato de a bala de canhão ser mais pesada.A diferença das taxas é devida a resistência do ar.A força de resistência do ar foi ignorada no modelo dado em ${(4)}$ .Sob algumas circunstancias, um corpo em queda com massa ${m}$ , como uma pena com baixa densidade e formato irregular, encontra uma resistência do ar proporcional a sua velocidade instantânea ${v}$ .Se nessas circunstancias, tomarmos a direção positiva como orientada para baixo, a força resultante que age sobre a massa será dada por

$\displaystyle F=F_{1}+F_{2}=mg-kv \ \ \ \ \ (6)$

onde o peso ${F_{1}=mg}$ do corpo é a força que age na direção positiva e a resistência do ar ${ F_{2}=-kv }$ é uma força chamada amortecimento viscoso que age na direção oposta ou para cima.Veja a figura ${2}$ .

Figura 2:Corpos em queda com resistência do ar

Agora, como a velocidade ${v}$ esta relacionado com a aceleração ${a}$ atraves de ${a=\frac{dv}{dt}}$ , a segunda lei de Newton torna-se

$\displaystyle F=m\cdot a =m\cdot \frac{dv}{dt} \ \ \ \ \ (7)$

substituindo a equação ${(6)}$ em ${(7)}$ obtemos a equação diferencial de primeira ordem para a velocidade ${v(t)}$ do corpo no instante ${t}$ .

$\displaystyle m\frac{dv}{dt}=mg-kv \ \ \ \ \ (8)$

onde ${k}$ é uma constante de proporcionalidade positiva.

como a velocidade inicial do objeto é ${v_{0}}$ , um modelo para a velocidade do corpo que cai se expressa mediante o problema de com valor inicial:

$\displaystyle m\frac{dv}{dt}=mg-kv, \quad v(0)=v_{0} \ \ \ \ \ (9)$

a equação ${(9)}$ é uma equação diferencial linear,ao resolvermos, obtemos:

$\displaystyle v(t)=\dfrac{mg}{k}+\left(v_{0}-\dfrac{mg}{k}\right)e^{-kt/m} \ \ \ \ \ (10)$

considerando ${s=0 }$ quando ${t=0}$ podemos determinar a equação de movimento do objeto integrando ${v=\frac{ds}{dt}}$ em relação a ${t}$ .Assim obtemos

$\displaystyle s(t)=\int v(t)dt=\int\left[\dfrac{mg}{k}+\left(v_{0}-\dfrac{mg}{k}\right)e^{-kt/m}\right]dt$

$\displaystyle s(t)=\dfrac{mg}{k}t-\dfrac{m}{k}\left(v_{0}-\dfrac{mg}{k}\right)e^{-kt/m}+c \ \ \ \ \ (11)$

fazendo ${s=0 }$ e ${t=0 }$ teremos

$\displaystyle 0=-\dfrac{m}{k}\left(v_{0}-\dfrac{mg}{k}\right)+c\Rightarrow c=\dfrac{m}{k}\left(v_{0}-\dfrac{mg}{k}\right)$

Substituindo o valor da constante ${c}$ em ${(11)}$ teremos a equação de movimento:

$\displaystyle s(t)=\dfrac{mg}{k}t+\dfrac{m}{k}\left(v_{0}-\dfrac{mg}{k}\right)(1-e^{-kt/m}) \ \ \ \ \ (12)$

Exemplo 1 Um objeto que pesa ${4}$ N cai desde uma grande altura partindo do repouso.Se o ar exerce uma resistência de ${\frac{1}{2}v}$ N, onde ${v}$ é a velocidade em m/s,figura 3.Achar a velocidade ${v(t)}$ e a distancia percorrida ${s(t)}$ no instante de tempo ${t}$ .

Solução:Consideremos a direção positiva para baixo.

Figura 3:Corpo em queda do exemplo 1

De acordo a segunda Lei de Newton temos:

$\displaystyle m\dfrac{dv}{dt}=F_{1}-F_{2}$

onde ${m=\frac{P}{g}=\frac{4}{32}=\frac{1}{8}, \quad F_{1}=P=4N, \quad F_{2}=\frac{1}{2}v N}$

substituindo teremos a equação diferencial

$\displaystyle \dfrac{1}{8}\dfrac{dv}{dt}=4-\dfrac{1}{2}v \Rightarrow \dfrac{dv}{dt}=32-4v$

separando as variáveis e integrando temos:

$\displaystyle \int\dfrac{dv}{8-v}=\int4dt \Rightarrow -\ln(8-v)=4t+C_{1}$

usando a condição ${v(0)=0,}$ teremos ${C_{1}=-\ln 8}$ .logo, ao substituir este valor de ${C_{1}}$ e isolando ${v}$ temos:

$\displaystyle v(t)=8(1-e^{-4t})$

Para achar ${s(t)}$ resolve-se o problema de valor inicial:

$\displaystyle v(t)=\dfrac{ds}{dt}=8(1-e^{-4t}); \quad s(0)=0$

separando as variáveis e integrando, obtemos:

$\displaystyle s(t)=8(t+\dfrac{1}{4}e^{-4t})+C_{0}$

usando a condição inicial ${s(0)=0}$ , temos ${C_{0}=-2}$ .Portanto

$\displaystyle s(t)=8(t+\dfrac{1}{4}e^{-4t})-2$

Exemplo 2 Um objeto que pesa ${30}$ N se deixa cair desde uma altura de ${40}$ m, com uma velocidade inicial de ${3m/s}$ .Suponhamos que a resistência do ar é proporcional a velocidade do corpo.Se sabe que a velocidade limite deve ser de ${40m/s}$ .Encontrar:

a velocidade depois de ${8 }$ segundos;
a expressão para a posição do corpo no instante de tempo ${t}$ ;

Solução:De acordo a segunda Lei de Newton, temos:

$\displaystyle m\dfrac{dv}{dt}=mg-kv$

onde ${P=30N \Rightarrow m=\frac{P}{g}=\frac{30}{9,8}\cong 3kg}$

temos que ${v_{lim}=40 m/s}$ onde ${v_{lim}=\frac{mg}{k}}$ ;então:

$\displaystyle k=\dfrac{mg}{v_{lim}}=\dfrac{30}{40} \Rightarrow k=\dfrac{3}{4}Ns/m$

substituindo esses valores na segunda Lei de Newton temos:

$\displaystyle \dfrac{dv}{dt}+\dfrac{1}{4}v=10$

resolvendo a equação diferencial linear teremos:

$\displaystyle v=C_{1}e^{-t/4}+40$

com a condição inicial ${v(t)=v_{0}\Rightarrow v(0)=3m/s}$ , temos:

$\displaystyle 3=C_{1}+40 \Rightarrow C_{1}=-37$

então, a velocidade em qualquer instante de tempo ${t}$ é:

$\displaystyle v=-37e^{-t/4}+40$

Para ${t=8s}$ temos:

$\displaystyle v(t)=-37e^{-8/4}+40 \Rightarrow v=35m/s$

Para encontrar a posição do corpo temos ${v=\frac{ds}{dt}}$ , então:

$\displaystyle \dfrac{ds}{dt}=-37e^{-y/4}+40$

a equação acima é uma equação de variáveis separáveis, resolvendo teremos como solução:

$\displaystyle s(t)=148e^{-t/4}+40t+C_{2}$

Aplicando a condição inicial ${s(t)=s_{0}\Rightarrow s(0)=0}$ teremos ${C_{2}=-148}$

portanto,

$\displaystyle s(t)=148e^{-t/4}+40t-148$

Aplicação das equações diferenciais de primeira ordem.Circuitos elétricos

02/23/2016 9:41 am / 3 comentários em Aplicação das equações diferenciais de primeira ordem.Circuitos elétricos

— 3.3.Circuitos em série —

Um circuito consiste em um numero qualquer de elementos unidos por seus terminais, com pelo menos um caminho fechado através do qual a carga possa fluir.

Dois elementos estão em serie se:

Possuem somente um terminal em comum(isto é, um terminal de um esta conectado somente a um terminal do outro).
O ponto comum entre os dois elementos não esta conectado a outro elemento percorrido por corrente

Neste artigo, examinaremos dois tipos de circuitos em serie:um circuito compreendendo um resistor e um capacitor e outro circuito formado por um resistor e um indutor.Estes circuitos são denominados, respetivamente, circuitos ${RC}$ e ${RL}$ , e apesar de sua simplicidade tem inúmeras aplicações em eletrónica, comunicações e sistemas de controle.

A análise de circuitos ${RC}$ e ${RL}$ aplicando as leis de Kirchhoff produz equações diferenciais.As equações diferenciais resultantes da analise de circuitos ${RC}$ e ${RL}$ são de primeira ordem, consequentemente, os circuitos são conhecido coletivamente como circuitos de primeira ordem.

Consideremos um circuito em serie contendo somente um resistor e um indutor, a segunda lei de Kirchhoff diz que a soma da queda de tensão no indutor ( ${ L\frac{di}{dt} }$ ) e da queda de tensão no resistor ( ${ iR }$ ) é igual a voltagem ( ${ E(t) }$ ) no circuito.Veja a figura 1;

Figura 1:Circuito em série RL

Logo, obtemos a equação diferencial linear para a corrente ( ${ i(t) }$ ).

$\displaystyle L\dfrac{di}{dt}+Ri=E(t) \ \ \ \ \ (1)$

em que L e R são constante conhecidas como a indutância e a resistência, respetivamente.A corrente é algumas vezes chamada de resposta do sistema.

A queda de potencial em um capacitor com capacitância ${ C }$ é dada por ${\frac{q(t)}{C}}$ , em que q é a carga no apacitor.Então, para o circuito em serie mostrado na figura 2, a segunda lei de Kirchhoff nos dá

$\displaystyle Ri+\frac{1}{C}q=E(t) \ \ \ \ \ (2)$

Figura 2:Circuito em série RC

Mas a corrente ${i}$ e a carga ${q}$ estão relacionados por ${ i=\frac{dq}{dt} }$ , logo, torna-se a equação diferencial linear

$\displaystyle R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t) \ \ \ \ \ (3)$

Exemplo 1 Um circuito ${RL}$ tem uma fem de ${5}$ voltes, uma indutância de ${1}$ henry, uma resistência de ${80}$ ohm e não tem corrente inicial.Determinar a corrente no circuito para qualquer instante de tempo ${t}$ .

Solução:A quantidade de corrente ${i}$ no circuito é:

$\displaystyle \dfrac{di}{dt}+\dfrac{R}{L}i=\dfrac{E}{L}$

sabemos que ${ E=5V ,\quad L=1H, \quad R=80\Omega }$ ,então a equação do circuito será:

$\displaystyle \dfrac{di}{dt}+80i=5$

resolvendo a equação diferencial linear acima temos:

$\displaystyle i=\dfrac{1}{16}+ce^{-80t}$

o exemplo diz que o circuito não tem corrente inicial, ou seja, para ${t=0 \Rightarrow i=0}$ , então: ${ c=-\dfrac{1}{16} }$

assim, a corrente em qualquer instante de tempo ${t}$ é:

$\displaystyle i=\dfrac{1}{16}-\dfrac{1}{16}e^{-80t}\Rightarrow i=\dfrac{1}{16}(1-e^{-80t})$

Exemplo 2 Um circuito ${RC}$ tem uma fem de ${200 \cos 2t}$ volt, uma resistência de ${50}$ ohm e uma capacitância de ${10^{-2}}$ farad. Em t=0 não há carga no condensador.Achar a corrente no circuito no instante ${t}$ .

Solução:A equação para a quantidade de carga electrica ${q}$ é:

$\displaystyle \dfrac{dq}{dt}+\dfrac{1}{RC}q=\dfrac{E}{R}$

sabemos que ${E=(200\cos 2t)V, \quad R=50\Omega, \quad C=10^{-2}F}$ , então a equação do circuito será:

$\displaystyle \dfrac{dq}{dt}+2q=4 \cos2t$

resolvendo a equação diferencial linear acima temos:

$\displaystyle q= \cos 2t + \sin 2t + ce^{-2t}$

Para ${t=0, \quad q=0;}$ então: ${c=-1}$

Para determinarmos a corrente temos que ter em mente que:

$\displaystyle i=\dfrac{dq}{dt}$

e uma vez obtida a carga, podemos encontrar a corrente:

$\displaystyle i=\dfrac{dq}{dt}=-2 \sin 2t + 2 \cos 2t + 2e^{-2t}$

Aplicações das equações diferenciais de primeira ordem.

02/17/2016 12:30 am / Deixe um comentário

— 3. Aplicações das equações diferenciais de primeira ordem. —

Em ciências, engenharia, economia e ate mesmo em psicologia, frequentemente desejamos descrever ou modelar o comportamento de algum sistema ou fenómeno em termos matemáticos.

A construção de um modelo matemático de um sistema começa com:

a identificação das variáveis responsáveis pela variação do sistema.Podemos a principio optar por não incorporar todas essa variáveis no modelo.Nesta etapa, estamos especificando o nível de resolução do modelo.
a elaboração de um conjunto de hipóteses razoáveis sobre o sistema que estamos tentando descrever.As hipóteses também incluem algumas leis empíricas que são aplicáveis ao sistema.

A estrutura matemática de todas essas hipóteses, ou o modelo matemático do sistema, é muitas vezes uma equação diferencial ou um sistema de equações diferenciais.Esperamos que um modelo matemático razoável do sistema tenha uma solução que seja consistente com o comportamento conhecido do sistema.Porem se as predições obtidas pela solução forem pobres, poderemos elevar o nível de resolução do modelo ou levantar hipóteses alternativas sobre o mecanismo de mudança do sistema.As etapas do processo de modelagem são então repetidas, conforme disposto no diagrama da Figura 1.

Figura 1:Diagrama para criar modelos matemáticos

Naturalmente, aumentando a resolução aumentaremos a complexidade do modelo matemático e, assim, a probabilidade de não conseguirmos obter uma solução explicita.

Um modelo matemático de um sistema físico frequentemente envolve a variável tempo t.Uma solução do modelo oferece então o estado do sistema; em outras palavras, os valores da variável (ou variáveis) para valores apropriados de t descrevem o sistema no passado, presente e futuro.

— 3.1. Crescimento e decrescimento —

O modelo mais simples de crescimento populacional é aquele em que se supõe que a taxa de crescimento de uma população ${\frac{dx}{dt}}$ é proporcional a população presente naquele instante ${x(t)}$ ,ou seja, quanto mais pessoas houver em um instante t, mais pessoas existirão no futuro. Podemos descrever o problema de encontrar ${x(t)}$ como o problema de valor inicial

$\displaystyle \dfrac{dx}{dt}=kx, \quad x(t_{0})=x_{0}, \quad x=x_{0}e^{kt} \ \ \ \ \ (1)$

onde k é uma constante de proporcionalidade, serve como modelo para diversos fenómenos envolvendo crescimento ou decrescimento

Exemplo 1.Em uma cultura, há inicialmente ${P_{0}}$ bactérias.Uma hora depois, t=1 o numero de bactérias passa a ser ${(3/2)P_{0}}$ .Se a taxa de crescimento é proporcional ao numero de bactérias presentes, determine o tempo necessário para que o numero de bactérias triplique

Solução:Primeiro resolvemos a equação diferencial

$\displaystyle \dfrac{dP}{dt}=kP$

sujeita a ${P(0)=P_{0}}$ .Então, usamos a condição empírica ${P(1)=(3/2)P_{0}}$ para determinar a constante de proporcionalidade k.Resolvendo a equação diferencial acima temos:

$\displaystyle \int \dfrac{dP}{P}=\int kdt\Rightarrow ln P=kt+c$

$\displaystyle P=e^{kt+c} \Rightarrow P(t)=ce^{kt}$

Em ${t=0}$ concluímos que

$\displaystyle P_{0}=ce^{0}=c$

assim, teremos:

$\displaystyle P(t)=P_{0}e^{kt}$

Em ${t=1}$ , temos:

$\displaystyle \frac{3}{2}P_{0}=P_{0}e^{kt}\Rightarrow e^{k}=\frac{3}{2}\Rightarrow k=ln (3/2)\Rightarrow k=0,4055$

A expressão N(t) é portanto

$\displaystyle P(t)=P_{0}e^{0,4055t}$

para encontrar o tempo necessário para que o numero de bactérias seja triplicado, resolvemos:

$\displaystyle 3P_{0}=P_{0}e^{0,4055t}\Rightarrow t=\dfrac{ln 3}{0,4055}\Rightarrow t=2,71horas$

Figura 2:Tempo que o numero de bactérias triplica

Como mostrado na Figura 3, a função exponencial ${e^{kt}}$ cresce com o tempo quando ${k>0}$ , e decresce quando ${k<0.}$ Logo, problemas que descrevem crescimentos, como população, bactéria ou mesmo capital, são caraterizados por um valor positivo de k; por outro lado, problemas, como desintegração radioativa, conduzem a um valor negativo de k.

Figura 3:Crescimento ${k>0}$ e decrescimento ${k<0.}$

Exemplo 2.A população de uma cidade cresce a uma taxa proporcional á população em qualquer tempo.Sua população inicial de 500 habitantes aumenta ${15^{o}/_{o}}$ em 10 anos.Qual será a população em 30 anos?

Solução:Primeiro resolvemos a equação diferencial

$\displaystyle \dfrac{dP}{dt}=kP, \quad P(0)=500$

Resolvendo a equação diferencial acima obtemos:

$\displaystyle P(t)=ce^{kt}$

Aplicando a condição inicial

$\displaystyle P(0)=500$

na equação acima temos:

$\displaystyle 500=ce^{k0}\Rightarrow c=500$

Então,

$\displaystyle P(t)=500e^{kt}$

sabemos que população inicial de 500 habitantes aumenta ${15^{o}/_{o}}$ ,ou seja, 75 habitantes em 10 anos,isto quer que depois de 10 anos a cidade tem 575 habitantes.logo,

$\displaystyle P(10)=575\Rightarrow 575=500e^{k10}\Rightarrow k=\frac{1}{10}ln 1.15$

já temos o valor de k, agora podemos determinar a população em 30 anos:

$\displaystyle P(30)=500e^{30(\frac{1}{10}ln 1.15)}\Rightarrow P(30)=760$

em 30 anos a cidade terá 760 habitantes.

— 3.2. Resfriamento —

A lei de resfriamento de Newton diz que a taxa de variação de temperatura ${T(t)}$ de um corpo em resfriamento é proporcional a diferença entre temperatura do corpo ${T}$ e a temperatura constante ${T_{m}}$ do meio ambiente, isto é:

$\displaystyle \dfrac{dT}{dt}=k(T-T_{m}) \ \ \ \ \ (2)$

em que k é uma constante de proporcionalidade.

Exemplo 3.Quando um bolo é retirado do forno, sua temperatura é de 300ºF.Tres minutos depois, sua temperatura passa para 200ºF.Quanto tempo levara para sua temperatura chegar a 75graus, se a temperatura do meio ambiente em que ele foi colocado for de exatamente 70ºF?

Solução:Com base a lei de resfriamento de Newton temos:

${T_{m}=70^{o}F}$ é a temperatura do meio ambiente;
T é a temperatura do bolo;

Devemos então resolver o problema de valor inicial

$\displaystyle \dfrac{dT}{dt}=k(T-T_{m}), \quad T(0)=300^{o}F$

e determinar o valor de K para que ${T(3)=200^{o}F.}$

A equação acima é linear e separável.Separando as variáveis, temos

$\displaystyle \dfrac{dT}{T-70}=kdt\Rightarrow ln |T-70|=kt+c_{1}$

$\displaystyle T-70=e^{kt+c_{1}}\Rightarrow T=70+c_{2}e^{kt}$

quando ${t=0, \quad T=300}$ .substituindo na ultima expressão teremos:

$\displaystyle 300=70+c_{2}e^{k0}\Rightarrow c_{2}=230$

Então,

$\displaystyle T=70+230e^{kt}$

agora estamos em condições para determinar o valor de k para ${T(3)=200}$ , de modo que teremos

$\displaystyle 200=70+230e^{k3}\Rightarrow e^{k3}=\dfrac{130}{230}\Rightarrow k=\frac{1}{3}ln \frac{13}{23}=-0,191018$

Então,

$\displaystyle T=70+230e^{-0,191018t}$

com base a ultima equação estamos em condições para achar o tempo ( ${t}$ ) que o bolo levara para atingir 75 graus ( ${T=75}$ ), fazendo:

$\displaystyle 75=70+230e^{-0,191018t}\Rightarrow e^{-0,191018t}=\dfrac{75-70}{230}\Rightarrow -0,191018t=ln \dfrac{5}{230}$

$\displaystyle t=20,13minutos$

Exemplo 4.Um termómetro é retirado de dentro de uma sala e colocado do lado de fora, em que a temperatura é de ${5^{0}C}$ .Após 1 minuto, o termómetro marcava 55ºC; após 5 minutos, 30ºC.Qual é a temperatura da sala? Solução:se

${T_{m}=5^{o}C}$ é a temperatura do ar;
${T}$ é a temperatura da sala;

então:

$\displaystyle \dfrac{dT}{dt}=k(T-5) \Rightarrow T=5+c_{2}e^{kt}$

se ${T(1)=55^{o}C}$ teremos

$\displaystyle 55=5+c_{2}e^{k1}\Rightarrow c_{2}e^{k}=50\Rightarrow c_{2}=50e^{-k}$

e se ${T(5)=30^{o}C}$ teremos

$\displaystyle 30=5+c_{2}e^{k5}\Rightarrow c_{2}e^{5k}=25$

substituindo ${c_{2}=50e^{-k}}$ na ultima expressão teremos

$\displaystyle 50e^{-k}e^{5k}=25\Rightarrow e^{4k}=\dfrac{25}{50}\Rightarrow k=-\dfrac{1}{4}ln 2$

o valor de ${c_{2}}$ será:

$\displaystyle c_{2}=50e^{-k}=50e^{-(-\frac{1}{4}ln 2 )}\Rightarrow c_{2}=59,4611$

então,

$\displaystyle T=5+59,4611e^{-\frac{1}{4}tln 2}$

agora podemos determinar a temperatura da sala no instante inicial, substituindo ${t=0}$ na equação acima,onde:

$\displaystyle T(0)=64,4611^{o}C$

Equações diferenciais de Bernoulli e Ricatti. Redução a separação de variáveis

02/10/2016 11:03 pm / 3 comentários em Equações diferenciais de Bernoulli e Ricatti. Redução a separação de variáveis

— 2.5. Equação de Bernoulli —

Neste artigo, não estudaremos nenhum tipo particular para equação diferencial.Consideraremos duas equações clássicas que podem ser transformadas em equações já estudadas nas seções anteriores e depois vamos abordar sobre redução a separação de variáveis.

Definição 14.A equação diferencial

$\displaystyle \dfrac{dy}{dx}+P(x)y=Q(x)y^{n} \ \ \ \ \ (11)$

em que n é um numero real qualquer, é chamada de equação de Bernoulli.Para ${n=0}$ e ${n=1}$ a equação (11) é linear em y.Agora se ${y\neq0}$ ,a equação (11) pode ser escrita da seguinte maneira:

$\displaystyle y^{-n}\dfrac{dy}{dx}+P(x)y^{1-n}=Q(x) \ \ \ \ \ (12)$

se fizermos ${w=y^{1-n},\quad n\neq0,\quad n\neq1,}$ então:

$\displaystyle \dfrac{dw}{dx}=(1-n)y^{-n}\dfrac{dy}{dx}$

com essa substituição, a equação (12) transforma-se na equação linear

$\displaystyle \dfrac{dw}{dx}+(1-n)P(x)w=(1-n)Q(x) \ \ \ \ \ (13)$

Resolvendo a equação (13) e depois fazendo ${y^{1-n}=w}$ , obtemos uma solução para a equação (11).

Exemplo 1.Resolva a seguinte equação

$\displaystyle \dfrac{dy}{dx}+\dfrac{1}{x}y=xy^{2}$

Solução:De acordo a equação de Bernoulli temos: ${P(x)=1/x,\quad Q(x)=x, \quad e \quad n=2}$ .logo, a mudança de variável

$\displaystyle w=y^{-1}\Rightarrow \dfrac{dw}{dx}=-y^{-2}\dfrac{dy}{dx}\Rightarrow \dfrac{dy}{dx}=-y^{2}\dfrac{dw}{dx}$

nos da o seguinte:

$\displaystyle -y^{2}\dfrac{dw}{dx}+\dfrac{1}{x}y=xy^{2}\Rightarrow \dfrac{dw}{dx}-\dfrac{1}{x}y^{-1}=-x$

substituindo ${w=y^{-1}}$ teremos:

$\displaystyle \dfrac{dw}{dx}-\dfrac{1}{x}w=-x$

o fator de integração para essa equação linear é:

$\displaystyle \mu(x)=e^{-\int \frac{dx}{x}}=e^{-ln x}=x^{-1}$

assim,multiplicando o fator de integração na equação linear, teremos:

$\displaystyle x^{-1}\dfrac{dw}{dx}-x^{-2}w=-1\Rightarrow \dfrac{d}{dx}(x^{-1}w)=-1$

integrando essa ultima forma, obtemos

$\displaystyle x^{-1}w=-x+c \quad ou \quad w=-x^{2}+cx$

como ${w=y^{-1}}$ , então ${y=\frac{1}{w}}$ ou

$\displaystyle y=\dfrac{1}{-x^{2}+cx}$

— 2.6. Equação de Ricatti —

Definição 15.A equação diferencial linear

$\displaystyle \dfrac{dy}{dx}=P(x)+Q(x)y+R(x)y^{2} \ \ \ \ \ (14)$

é chamada de equação de Ricatti.Se ${y_{1}}$ é uma solução particular para (14),então as substituições

$\displaystyle y=y_{1}+u \quad e \quad \dfrac{dy}{dx}=\dfrac{dy_{1}}{dx}+\dfrac{du}{dx}$

em (14) produzem a seguinte equação diferencial para u:

$\displaystyle \dfrac{du}{dx}-(Q+2y_{1}R)u=Ru^{2} \ \ \ \ \ (15)$

como (15) é uma equação de Bernoulli com ${n=2}$ , ela pode, por sua vez, ser reduzida a equação linear

$\displaystyle \dfrac{du}{dx}+(Q+2y_{1}R)u=-R \ \ \ \ \ (16)$

através da substituição ${w=u^{-1}}$ .Depois de fazer essa substituição podemos aplicar os outros métodos estudados.

Exemplo 2.Considere a equação

$\displaystyle \dfrac{dy}{dx}=e^{2x}+(1+2e^{x})y+y^{2}$

Verifica-se que ${y_{1}=-e^{x}}$ é uma solução particular desta equação.Fazendo a substituição

$\displaystyle y=-e^{x}+u\Rightarrow \dfrac{dy}{dx}=-e^{x}+\dfrac{du}{dx}$

teremos:

$\displaystyle -e^{x}+\dfrac{du}{dx}=e^{2x}+(1+2e^{x})(-e^{x}+u)+(-e^{x}+u)^{2}$

simplificando a equação obtemos a seguinte expressão

$\displaystyle \dfrac{du}{dx}=u+u^{2}$

a equação acima é uma equação de Bernouli, então,vamos fazer a seguinte substituição:

$\displaystyle w=u^{-1}\Rightarrow \dfrac{dw}{dx}=-y^{-2}\dfrac{du}{dx}\Rightarrow \dfrac{du}{dx}=-u^{2}\dfrac{dw}{dx}$

logo, teremos:

$\displaystyle -u^{2}\dfrac{dw}{dx}=u+u^{2}\Rightarrow \dfrac{dw}{dx}=-\dfrac{1}{u}-1\Rightarrow \dfrac{dw}{dx}=-w-1$

a ultima equação é de variáveis separáveis de modo que resolvendo teremos:

$\displaystyle ln (w+1)=-x+c_{1}\Rightarrow w=e^{-x+c_{1}}-1\Rightarrow w=ce^{-x}-1$

substituindo ${w=u^{-1}}$ temos:

$\displaystyle u^{-1}=ce^{-x}-1\Rightarrow u=\dfrac{1}{ce^{-x}-1}$

substituindo ${u=y+e^{x}}$ obtemos que a solução da equação é dada por:

$\displaystyle y=\dfrac{1}{ce^{-x}-1}-e^{x}$

— 2.7. Redução a Separação De Variáveis —

Definição 16.Uma equação diferencial da forma

$\displaystyle \dfrac{dy}{dx}=f(Ax+By+c)$

se pode sempre reduzir a uma equação com variáveis separáveis por meio da substituição ${u=Ax+By+c}$ , ${B\neq0}$

Exemplo 3.Resolva a seguinte equação diferencial

$\displaystyle \dfrac{dy}{dx}=(-2x+y)^{2}-7, \quad y(0)=0$

Solução:Vamos resolve-la fazendo a substituição

$\displaystyle u=-2x+y\Rightarrow \dfrac{du}{dx}=-2+\dfrac{dy}{dx}$

dessa maneira a equação diferencial se expressa da seguinte forma:

$\displaystyle \dfrac{du}{dx}+2=u^{2}-7\Rightarrow \dfrac{du}{dx}=u^{2}-9$

essa ultima equação é de variáveis separáveis de modo que teremos:

$\displaystyle \dfrac{du}{(u-3)(u+3)}=dx\Rightarrow \dfrac{1}{6}\left[\dfrac{1}{u-3}-\dfrac{1}{u+3}\right]du=dx$

e depois de integrar vamos ter:

$\displaystyle \dfrac{1}{6}ln \left[\dfrac{u-3}{u+3}\right]=x+c_{1}\Rightarrow \dfrac{u-3}{u+3}=e^{6x+6c_{1}}$

substituindo ${e^{6c_{1}}}$ por c e isolando u obtemos o seguinte:

$\displaystyle u=\dfrac{3(1+ce^{6x})}{1-ce^{6x}}$

substituindo ${u=-2x+y}$ na equação acima obtemos a seguinte solução:

$\displaystyle y=2x+\dfrac{3(1+ce^{6x})}{1-ce^{6x}}$

por ultimo aplicando a condição inicial ${y(0)=0}$ a ultima equação obtém-se ${c=-1}$ de modo que a solução particular será:

$\displaystyle y=2x+\dfrac{3(1-e^{6x})}{1+e^{6x}}$

a figura abaixo mostra em azul escuro o gráfico da solução particular junto com o gráfico de outros membros da família de soluções.

eqdf3

Figura 1:Algumas soluções do Exemplo 3

Nas seções precedentes, vimos que em certas situações uma equação diferencial podia ser ser transformada, por meio de uma substituição, em uma forma em que era possível resolve-la por um método padrão.Uma equação pode parecer diferente de todas as que vimos e estudamos, mas mudando uma variável, talvez um problema aparentemente difícil possa ser facilmente resolvido.Embora não haja uma regra geral que indique qual substituição deve ser feita,uma axioma pratico é o seguinte:tente alguma coisa!Algumas vezes custa caro ser engenhoso.

Exemplo 4.Considere a equação

$\displaystyle \dfrac{dy}{dx}=\dfrac{y-x}{y-x-1}$

se olharmos bem a equação, podemos ser impelidos a tentar a substituição

$\displaystyle u=y-x\Rightarrow \dfrac{du}{dx}=\dfrac{dy}{dx}-1\Rightarrow \dfrac{dy}{dx}=\dfrac{du}{dx}+1$

substituindo na equação temos:

$\displaystyle \dfrac{du}{dx}+1=\dfrac{u}{u-1}\Rightarrow \dfrac{du}{dx}=\dfrac{1}{u-1}\Rightarrow (u-1)\dfrac{du}{dx}=1$

que é uma equação de variável separável cuja solução é:

$\displaystyle \dfrac{u^{2}}{2}-u=x+c$

Substituindo-se de volta ${u=y-x}$ obtemos que a solução da equação é dada implicitamente por

$\displaystyle \dfrac{(y-x)^{2}}{2}-y=c$

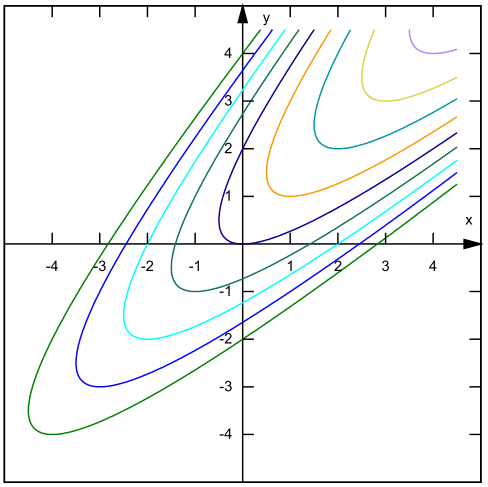
eqdf4

Figura 2:soluções da equação do Exemplo 4

Equações Diferenciais Exatas e Lineares

02/08/2016 12:14 am / Deixe um comentário

— 2.3. Equações Diferenciais Exatas —

Definição 11. Uma expressão diferencial

$\displaystyle M(x,y)dx+N(x,y)dy$

é uma diferencial exata em uma região do plano xy se ela corresponde á diferencial total de alguma função f(x,y).Uma equação diferencial da forma

$\displaystyle M(x,y)dx+N(x,y)dy=0$

é chamada de uma equação exata se a expressão do lado esquerdo é uma diferencial exata

Teorema 2 Sejam M(x,y) e N(x,y) funções continuas com derivadas parciais continuas em uma região retangular R definida por ${ a<x<b, c<y<d. }$ Então, uma condição necessária e suficiente para que

$\displaystyle M(x,y)dx+N(x,y)dy$

seja uma equação diferencial exata é

$\displaystyle \dfrac{\partial M}{\partial y}=\dfrac{\partial N}{\partial x}$

— 2.3.2. Método de solução —

Dada a equação

$\displaystyle M(x,y)dx+N(x,y)dy=0 \ \ \ \ \ (1)$

mostre primeiro que

$\displaystyle \dfrac{\partial M}{\partial y}=\dfrac{\partial N}{\partial x} \ \ \ \ \ (2)$

Depois suponha que

$\displaystyle \dfrac{\partial f}{\partial x}=M(x,y) \ \ \ \ \ (3)$

dai podemos encontrar f integrando M(x,y) com relação a x, considerando y constante, escrevemos:

$\displaystyle f(x,y)=\int M(x,y)dx+g(y) \ \ \ \ \ (4)$

em que a função arbitraria g(y) é a constante de integração.Agora, derivando a equação (4) com relação a y e supondo ${\partial f/\partial y=N(x,y):}$

$\displaystyle \dfrac{\partial f}{\partial y}=\dfrac{\partial}{\partial y}\int M(x,y)dx+g\prime(y)=N(x,y). \ \ \ \ \ (5)$

Assim

$\displaystyle g\prime(y)=N(x,y)-\dfrac{\partial}{\partial y}\int M(x,y)dx \ \ \ \ \ (6)$

Finalmente podemos integrar a equação (6) com relação a y e substituir o resultado em (4).A solução para a equação é ${f(x,y)=c}$

Nota:Poderíamos também começar o procedimento acima com a suposição de que ${ \partial f/\partial y=N(x,y). }$ Depois, integrando N com relação a y e derivando o resultado, encontramos o análogo de (4) e (6), que seria respetivamente.

$\displaystyle f(x,y)=\int N(x,y)dy+h(x) \quad h\prime(x)=M(x,y)-\dfrac{\partial}{\partial x}\int N(x,y)dy$

Exemplo 1.Resolva a seguinte equação

$\displaystyle (6xy-2y^{2})dx+(3x^{2}-4xy)dy=0$

Solução.com ${M(x,y)=(6xy-2y^{2}) \quad N(x,y)=(3x^{2}-4xy)}$ temos

$\displaystyle \dfrac{\partial M}{\partial y}=6x-4y=\dfrac{\partial N}{\partial x}$

logo, a equação é exata e existe uma função f(x,y) tal que

$\displaystyle \dfrac{\partial f}{\partial x}=(6xy-2y^{2})$

depois de integrar em relação a x, obtemos:

$\displaystyle f(x,y)=3x^{2}y-2xy^{2}+g(y)$

Derivando a ultima expressão com relação a y e igualando o resultado a N(x,y), temos

$\displaystyle \dfrac{\partial f}{\partial y}=3x^{2}-4xy+g\prime(y)=3x^{2}-4xy$

segue-se que

${g\prime(y)=0}$ integrando teremos ${g(y)=c}$

A constante de integração não precisa ser incluída, pois a solução é ${ f(x,y)=c}$ então

$\displaystyle 3x^{2}y-2xy^{2}=c$

OBS:Poderíamos resolver também supondo que ${\dfrac{\partial f}{\partial y}=(3x^{2}-4xy)}$

— 2.3.3. Equações diferenciais exatas com fator de Integração —

Definição 12. Se existe uma função ${\mu(x,y)}$ tal que

$\displaystyle \mu(x,y)M(x,y)dx+\mu(x,y)N(x,y)dy=0$

é exata, então ${\mu(x,y)}$ chama-se fator de integração da equação diferencial

$\displaystyle M(x,y)dx+N(x,y)dy=0$

Quando a expressão ${M(x,y)dx+N(x,y)dy=0}$ não é diferencial exata, isto é,

$\displaystyle \dfrac{\partial M}{\partial y}\neq\dfrac{\partial N}{\partial x} ,$

mostra-se que há uma infinidade de funções ${\mu(x,y),}$ tais que

$\displaystyle \mu(Mdx+Ndy).$

Se o fator de integração é em função de x temos:

$\displaystyle \mu(x)=e^{\int P(x)} \Rightarrow P(x)=\dfrac{1}{N}\left( \dfrac{\partial M}{\partial y}-\dfrac{\partial N}{\partial x}\right)$

Se o fator de integração é em função de y temos:

$\displaystyle \mu(y)=e^{\int P(y)} \Rightarrow P(y)=\dfrac{1}{M}\left(\dfrac{\partial N}{\partial x}-\dfrac{\partial M}{\partial y}\right)$

Exemplo 2.Encontrar o fator de integração de:

$\displaystyle 3x^{2}ydx+ydy=0$

Solução:Para acharmos o fator de integração temos de verificar se o fator de integração será em função de “x” ou “y”.Para isso vamos determinar primeiro as seguintes derivadas parciais:

$\displaystyle \dfrac{\partial M}{\partial y}=3x^{2} \quad \dfrac{\partial N}{\partial x}=0$

vamos provar se ${\mu(x)}$ é o fator de integração:

${P(x)=\dfrac{1}{N}\left( \dfrac{\partial M}{\partial y}-\dfrac{\partial N}{\partial x}\right)=\dfrac{3x^{2} }{y}}$ é uma função de x,logo a função ${\mu(x)}$ não é o fator de integração capaz de converter a equação diferencial em uma exata.

por isso vamos achar ${\mu(y)}$ com:

${P(y)=\dfrac{1}{M}\left(\dfrac{\partial N}{\partial x}-\dfrac{\partial M}{\partial y}\right)=\dfrac{0-3x^{2}}{3x^{2}y}=-\dfrac{1}{y},}$ é uma função de y,então a função ${\mu(y)}$ é o fator de integração capaz de converter a equação diferencial em uma exata.Nesse caso, teremos:

${\mu(y)=e^{\int -\dfrac{dy}{y}}=e^{-ln y}=\dfrac{1}{y}}$ com ${y\neq0}$

multiplicando a equação diferencial com este fator teremos:

$\displaystyle 3x^{2}dx+dy=0 \quad M=3x^{2} \quad N=1$

logo:

$\displaystyle \dfrac{\partial N}{\partial x}=\dfrac{\partial M}{\partial y}=0$

agora a equação é exata e existe uma função tal que:

${\dfrac{\partial f}{\partial x}=3x^{2} \Rightarrow f=x^{3}+g(y)}$ derivando em relação a y e igualando a ${\frac{\partial f}{\partial y}=1}$ temos:

$\displaystyle \dfrac{\partial f}{\partial y}=g\prime(y)=1 \Rightarrow g(y)=y \Rightarrow f=x^{3}+y$

então:

$\displaystyle x^{3}+y=c$

a família de curvas da solução para alguns valores de c é:

eqdf2

Figura 1:Família de curvas da solução do Exemplo 2

— 2.4. Equações lineares —

Definição 13. Uma equação diferencial linear de 1ª ordem tem a forma:

$\displaystyle \dfrac{dy}{dx}+P(x)y=Q(x) \ \ \ \ \ (7)$

se ${Q(x)=0}$ , a equação é dita homogénea ou incompleta; enquanto,

se ${Q(x)\neq0}$ , a equação é dita não homogénea ou completa.

Analisaremos dois métodos de solução de equações diferenciais desse tipo a saber:

Método do fator integrante
Método de Lagrange

— 2.4.4. Método do Fator Integrante —

Este método consiste na transformação de uma equação linear em outra equação do tipo diferencial exata, cuja solução já estudamos anteriormente.Dessa maneira, vamos retornar a equação original de nosso problema

$\displaystyle \dfrac{dy}{dx}+P(x)y=Q(x)$

vamos reescrever esta ultima sob a forma

$\displaystyle (Py-Q)dx+dy=0$

multiplicando ambos os membros por ${e^{\int Pdx}}$ (fator integrante) obtemos a expressão:

$\displaystyle e^{\int Pdx}(Py-Q)dx+e^{\int Pdx}dy=0$

Identificando as funções M e N temos:

$\displaystyle M=e^{\int Pdx}(Py-Q) \quad N=e^{\int Pdx}$

derivando M em relação a e N com relação a x, obtemos:

$\displaystyle \dfrac{\partial M}{\partial y}=Pe^{\int Pdx} \quad \dfrac{\partial N}{\partial x}=Pe^{\int Pdx}$

confirmando assim, que a equação transformada é uma equação diferencial exata.

Exemplo 3.Resolve pelo método do fator integrante a seguinte equação:

$\displaystyle \dfrac{dy}{dx}+\dfrac{2}{x}y=x$

Solução:sabemos que ${P(x)=\dfrac{2}{x} \quad Q(x)=x,}$ então o fator integrante é

$\displaystyle \mu(x)=e^{\int \frac{2}{x}dx}=e^{2ln x}=x^{2}$

multiplicando a equação acima pelo fator integrante obtemos:

$\displaystyle x^{2}\dfrac{dy}{dx}+2xy=x^{3}$

o lado esquerdo é igual a derivada do produto ${x^{2}y}$ .Logo a equação acima é equivalente a:

$\displaystyle \dfrac{d}{dx}\left(x^{2}y\right) =x^{3}$

Integrando-se temos:

$\displaystyle x^{2}y=\dfrac{x^{4}}{4}+c$

explicitando y temos que a solução geral da equação diferencial é

$\displaystyle y=\dfrac{x^{2}}{4}+\dfrac{c}{x^{2}}$

podemos esboçar as soluções desta equação diferencial.Para ${c=0}$ a solução é a parábola

$\displaystyle y=\dfrac{x^{2}}{4}$

para ${c\neq0}$ ,temos que o domínio de y é o conjunto dos números reais tais que ${x\neq0}$

$\displaystyle \lim_{x\rightarrow \pm \infty}y(x)=+\infty \quad c\neq0$

além disso

$\displaystyle \lim_{x\rightarrow0}y(x)=+\infty \quad se \quad c>0$

$\displaystyle \lim_{x\rightarrow0}y(x)=-\infty \quad se \quad c<0$

vamos analisar o crescimento e decrescimento das soluções

$\displaystyle \dfrac{dy}{dx}=\dfrac{x}{2}-\dfrac{2c}{x^{3}}=0$

se, e somente se ${x^{4}=4c}$

assim se ${c>0}$ as soluções tem somente pontos críticos em ${x=\pm\sqrt[4]{4c}}$ e se ${c<0}$ elas não tem ponto critico.

eqdf1

Figura 2: Soluções da equação do Exemplo 3

— 2.4.5. Método de Lagrange —

Esse método consiste na substituição de “y” por “Z.t” na equação (7), onde ${ t=\phi(x)}$ e ${z=\psi(x)}$ sendo z a nova função incógnita e t a função a determinar, assim ${y=z.t}$

Derivando em relação a x temos:

$\displaystyle \dfrac{dy}{dx}=z\dfrac{dt}{dx}+t\dfrac{dz}{dx} \ \ \ \ \ (8)$

substituindo (8) em (7) vamos obter:

$\displaystyle z\dfrac{dt}{dx}+t\dfrac{dz}{dx}+Pzt=Q$

$\displaystyle z\left(\dfrac{dt}{dx}+Pt\right)+t\dfrac{dz}{dx}=Q \ \ \ \ \ (9)$

Para integral a equação (9), examina-se dois casos particulares da equação (7) a saber:

P=0, então ${\dfrac{dy}{dx}=Q}$ (não homogénea) logo: ${y=\int Qdx+c}$
Q=0, então ${\dfrac{dy}{dx}+Py=0}$ (equação homogénea) que resulta em:

${dy+Pydx=0}$ que é uma equação de variáveis separáveis.

daí, ${\dfrac{dy}{y}+Pdx=0}$ integrando essa equação resulta em

$\displaystyle ln y=c-\int Pdx \Rightarrow y=e^{c-\int Pdx}=e^{c}e^{-\int Pdx}$

Fazendo ${k=e^{c}}$ , temos ${y=ke^{c-\int Pdx}}$ que representa a solução homogénea ou incompleta.

Agora, vamos pesquisar na equação (9) valores para “t” e “z”, uma vez que ${y=z.t}$ , teremos a solução da equação (7) que é uma equação linear completa (não homogénea).

Na equação (9) vamos impor o coeficiente de z como sendo nulo.

$\displaystyle \dfrac{dt}{dx}+Pt=0$

como já estudamos no caso 2 teremos: ${t=ke^{-\int Pdx},}$ substituindo este resultado em

$\displaystyle t\dfrac{dz}{dx}=Q$

temos

$\displaystyle ke^{-\int Pdx}\dfrac{dz}{dx}=Q \Rightarrow dz=\dfrac{1}{k}e^{\int Pdx}Qdx$

integrando este ultimo resultado temos:

$\displaystyle z=\dfrac{1}{k}\int e^{\int Pdx}Qdx+c$

lembrando que ${y=z.t}$ vamos obter, substituindo “t” e “z”:

$\displaystyle y=ke^{-\int Pdx}\left[ \dfrac{1}{k}\int e^{\int Pdx}Qdx+c\right]$

onde resulta, finalmente em:

$\displaystyle y=e^{-\int Pdx}\left[\int e^{\int Pdx}Qdx+c\right] \ \ \ \ \ (10)$

que é a solução geral da equação

Exemplo 4.Resolver pelo método de Lagrange a seguinte equação:

$\displaystyle y\prime=2y+x$

Solução:Nota-se que a equação ${y\prime-2y=x}$ é linear, onde:

$\displaystyle P(x)=-2 \quad Q(x)=x.$

A equação diferencial homogénea correspondente é ${y\prime-2y=0}$ que tem como solução: ${y=ce^{2x}}$

fazendo ${z=c}$ e ${t=e^{2x}}$ acharemos a função z dada por:

$\displaystyle z=\int e^{\int Pdx}Qdx+c=\int e^{-\int 2dx}xdx+c=-\dfrac{x}{2}e^{-2x}-\dfrac{1}{4}e^{-2x}+c$

como a solução da equação homogénea é ${y=zt}$ ,então

$\displaystyle y=\left(-\dfrac{x}{2}e^{-2x}-\dfrac{1}{4}e^{-2x}+c\right)e^{2x} \Rightarrow y=-\dfrac{x}{2}-\dfrac{1}{4}+ce^{2x}$

2. Equações Diferenciais de Primeira ordem

02/03/2016 10:44 pm / Deixe um comentário

— 2. Equações Diferenciais de Primeira ordem —

Existem alguns tipos de equações ordinárias de primeira ordem que podem ser resolvidas analiticamente.Comecemos por estudar o caso mais simples das equações diferenciais de primeira ordem e depois analisaremos as equações de variáveis separáveis e as equações homogéneas.

O caso mais simples das equações diferenciais de primeira ordem tem a seguinte forma:

${\dfrac{dy}{dx}=f(x)}$

resolve-se facilmente, usando o teorema do calculo integral

$\displaystyle y(x)=\int f(x)dx+c$

em que c é uma constante arbitraria que será determinada segundo a condição inicial do problema

OBS:Na resolução de uma equação diferencial, você terá frequentemente que utilizar, integração por partes, frações parciais ou possivelmente uma substituição.Será proveitoso gastar alguns minutos de seu tempo na revisão de algumas técnicas de integração.

— 2.1. Equações Diferenciais de Variáveis Separáveis —

Definição 9.Uma equação diferencial de variáveis separáveis tem a forma

${f(x)dx+g(y)dy=0}$

onde cada diferencial tem como coeficiente uma função de sua própria variável, ou uma constante.

Metodo de solução:Integraçã direta

${\int f(x)dx+\int g(y)dy=0}$

Deve-se ter em conta que quando não a maneiras de separar as variáveis, deve-se usar outros métodos para encontrar a solução.

Exemplo 1.Resolva ${(1+x)dy-ydx=0}$

Solução:Dividindo a equação por ${(1+x)y}$ , podemos escrever

$\displaystyle \dfrac{dy}{y}-\dfrac{dx}{1+x}=0$

onde teremos:

$\displaystyle \int\dfrac{dy}{y}=\int\dfrac{dx}{1+x}\Rightarrow ln |y|=ln |1+x|+c_{1}$

$\displaystyle y=e^{ln |1+x|+c_{1}}=e^{ln |1+x|}.e^{c_{1}}$

$\displaystyle y=|1+x|.e^{c_{1}}\Rightarrow y=\pm e^{c_{1}}(1+x)$

fazendo ${ c=\pm e^{c_{1}} }$ teremos:

${y=c(1+x)}$

Exemplo 2. Resolva o problema de valor inicial

$\displaystyle \dfrac{dy}{dx}=-\dfrac{x}{y} \quad y(4)=3$

Solução:De ${ydy=-xdx }$ , obtemos

$\displaystyle \int ydy=-\int xdx \Rightarrow \dfrac{y^{2}}{2}=-\dfrac{x^{2}}{2}+c_{1}$

Essa solução pode ser escrita como

$\displaystyle x^{2}+y^{2}=c^{2}$

trocando as constantes ${ 2c_{1} }$ por ${ c^{2}.}$ A solução representa uma família de círculos concêntricos. Agora, quando ${x=4, y=3}$ temos ${16+9=25=c^{2}}$ logo, o problema de valor inicial determina

${ x^{2}+y^{2}=25}$

Em vista do teorema de Picard, podemos concluir que este é o único circulo da família que passa pelo ponto ${(4,3)}$

Exemplo 3. Resolva ${\dfrac{dy}{dx}=\dfrac{xy+2y-x-2}{xy-3y+x-3}}$ Solução: Aplicando factorização teremos:

$\displaystyle \dfrac{dy}{dx}=\dfrac{y(x+2)-(x+2)}{y(x-3)+(x-3)}\Rightarrow \dfrac{dy}{dx}=\dfrac{(x+2)(y-1)}{(x-3)(y+1)}$

Colocando a equação na forma: ${ \dfrac{y+1}{y-1}dy=\dfrac{x+2}{x-3}dx }$ ou

$\displaystyle \left(1-\dfrac{2}{y-1}\right)dy=\left( 1+\dfrac{5}{x-3}\right) dx$

nos obtemos:

$\displaystyle y+2ln |y-1|=x+5ln |x-3|+c$

${\dfrac{(y-1)^{2}}{(x-3)^{5}}=c_{1}e^{x-y}}$

— 2.2. Equações Diferenciais Homogéneas —

Definição 10:Uma equação diferencial ${ M(x,y)dx+N(x,y)dy=0 }$ é dita homogénea se ambos os coeficientes M e N são funções homogéneas do mesmo grau, ou seja, se:

${ M(tx,ty)=t^{n}M(x,y) \quad N(tx,ty)=t^{n}N(x,y)}$

— 2.2.1. Método de solução —

Uma equação diferencial homogénea ${ M(x,y)dx+N(x,y)dy=0 }$ , pode ser resolvida por meio de uma substituição algébrica.Para transformar a equação em uma equação de variáveis separáveis usamos a substituição ${y=xu}$ ou ${ x=vy }$ em que u e v são as novas variáveis independentes.Se usarmos a substituição ${y=xu}$ seu diferencial será ${dy=udx+xdu}$ e se usarmos ${ x=vy }$ seu diferencial será ${dx=vdy+ydv}$ .

Exemplo 4.Resolva ${(x^{2}+y^{2})dx+(x^{2}-xy)dy=0}$

Solução: Primeiro passo é verificar se as funções são homogéneas do mesmo grau.

$\displaystyle M(tx,ty)=(t^{2}x^{2}+t^{2}y^{2}) \quad N(tx,ty)=(t^{2}x^{2}-t^{2}xy)$

Nota-se que tanto M e N são homogéneas de grau dois. Segundo passo será fazer a substituição.Se fizermos ${y=xu}$ teremos:

$\displaystyle (x^{2}+u^{2}x^{2})dx+(x^{2}-ux^{2})[udx+xdu]=0$

Terceiro passo será arrumar a equação e verificar que ficou separável

$\displaystyle x^{2}(1+u)dx+x^{3}(1-u)du=0 \Rightarrow \dfrac{1-u}{1+u}du+\dfrac{dx}{x}=0$

$\displaystyle \left[-1+\dfrac{2}{1+u}\right] du+\dfrac{dx}{x}=0$

Quarto passo será resolver a equação.Depois de integrar a ultima linha, obtemos:

$\displaystyle -u+2ln|1+u|+ln|x|=ln|c|$

Quinto passo será voltar a variável antiga, substituindo por ${u=\dfrac{y}{x}:}$

$\displaystyle \dfrac{-y}{x}+2ln|1+\dfrac{y}{x}|+ln|x|=ln|c|$

Usando as propriedades do logaritmo, podemos escrever a solução como

$\displaystyle ln|\dfrac{(x+y)^{2}}{cx}|=\dfrac{y}{x}$

A definição de um logaritmo implica

${ (x+y)^{2}=cxe^{y/x}}$

Existem outras equações que podem ser reduzidas a equações homogéneas mediante determinada troca de variáveis.Um exemplo típico é a equação

${\dfrac{dy}{dx}=f\left(\dfrac{ax+by+c}{px+qy+r}\right)}$

onde a,b,c,p,q e r são constantes dadas.Se as constantes c e r fossem nulas, a equação seria homogenea; definimos um novo sistema de coordenadas ${ (u,v) }$ para substituir ${ (x,y) }$ , de forma a obter

$\displaystyle \begin{array}{rc} ax+by+c=au+bv \\ px+qy+r=pu+qv \end{array}$

ou de forma equivalente

$\displaystyle \begin{array}{rc} a(x-u)+b(y-v)=-c\\ p(x-u)+q(y-v)=-r \end{array}$

A solução deste sistema de equações lineares pode ser obtido por meio da regra de cramer

$\displaystyle x-u=\dfrac{\begin{bmatrix} -c & b\\ -r & q \end{bmatrix}}{\begin{bmatrix} a & b\\ p & q \end{bmatrix}} \quad y-u=\dfrac{\begin{bmatrix} a & -c\\ p & -r \end{bmatrix}}{\begin{bmatrix} a & b\\ p & q \end{bmatrix}}$

como a,b,c,d,q e r são constantes e também ${dx=du \quad dy=dv}$ a equação diferencial converte-se numa equação homogénea

${\dfrac{dv}{du}=f\left(\dfrac{au+bv}{pu+qv}\right)}$

Exemplo 5.Resolva o problema de valor inicial

$\displaystyle \dfrac{dy}{dx}=f\left(\dfrac{x+y-3}{x-y-1}\right) \quad y(3)=1$

Solução:Esta equação pode ser reduzida a uma equação homogenea, mudando as variaveis (x,y) para (u,v) definidas por

$\displaystyle \begin{array}{ccc} x+y-3=u+v\\ x-y-1=u-v \end{array} \Rightarrow \begin{array}{ccc} (x-u)+(y-v)=3\\ (x-u)-(y-v)=1 \end{array}$

usando a regra de Cramer temos

$\displaystyle x-u=\dfrac{\begin{bmatrix} 3 & 1\\ 1 & -1 \end{bmatrix}}{\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix}}=2 \quad y-u=\dfrac{\begin{bmatrix} 1 & 3\\ 1 & 1 \end{bmatrix}}{\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix}}=1$

$\displaystyle \begin{array}{cc} x=u+2 \Rightarrow dx=du\\ y=v+1 \Rightarrow dy=dv \end{array}$

com estas substituições, a equação diferencial torna-se uma equação homogénea

$\displaystyle \dfrac{dv}{du}=\dfrac{u+v}{u-v}$

e para reduzir a equação de variáveis definimos uma nova variável dependente z

$\displaystyle z=\dfrac{v}{u} \Rightarrow \dfrac{dv}{du}=z+u\dfrac{dz}{du}$

substituindo na equação diferencial, teremos:

$\displaystyle z+u\dfrac{dz}{du}=\dfrac{1+z}{1-z}$

$\displaystyle \dfrac{dz}{du}=\dfrac{1}{u}\left(\dfrac{1+z}{1-z}-z\right)=\dfrac{z^{2}-1}{u(1-z)}$

esta equação de variáveis separáveis pode ser integrada

$\displaystyle \int\dfrac{1-z}{z^{2}+1}dz=\int\dfrac{du}{u}+c \Rightarrow \arctan (z)-\dfrac{1}{2}ln\left(1+z^{2}\right)=ln u +c$

para calcular o valor da constante c, vemos que a condição inicial

$\displaystyle y(3)=1 \Rightarrow u=2, v=0 \quad z=0$

então:

$\displaystyle \arctan 0-\dfrac{ln 1}{2}=ln 2 + c \Rightarrow \arctan (z)-\dfrac{1}{2}ln\left(1+z^{2}\right)=ln u$

e a solução em função de x e y é:

${\arctan \left(\dfrac{y-1}{x-2}\right)-\dfrac{1}{2}ln \left[1+\left(\dfrac{y-1}{x-2}\right)^{2}\right]=ln (x-2)}$

1. Exercícios Resolvidos de Equações Diferenciais

12/02/2015 5:40 pm / 1 comentário em 1. Exercícios Resolvidos de Equações Diferenciais

— 1. Exercícios Resolvidos de Equações Diferenciais —

Abordamos alguns conceitos básicos sobre equações diferencias, agora vamos resolver alguns exercícios relacionados ao assunto.

Exercício 1.Verifique se a função dada é uma solução para a equação diferencial.

${y\prime\prime-6y\prime+13y=0;}$ ${ y=e^{3x} \cos 2x}$
Solução:Da função ${y=e^{3x} \cos 2x}$ obtemos: ${y\prime=3e^{3x} \cos 2x - 2e^{3x}\sin 2x}$ ${\\ y\prime\prime=5e^{3x}\cos 2x - 12e^{3x}\sin 2x }$

Substituindo as derivadas na equação teremos:

$\displaystyle y\prime\prime-6y\prime+13y=(5e^{3x}\cos 2x - 12e^{3x}\sin 2x)-6(3e^{3x}\cos 2x - 2e^{3x}\sin 2x)+ 13(e^{3x} \cos 2x)=0$
${y\prime\prime+y=\tan x;}$ ${y=-(\cos x)\ln(\sec x+ tan x)}$
Solução:Da função ${y=-(\cos x)\ln(\sec x+ tan x) }$ obtemos: ${y\prime=-1+\sin x ln(\sec x +\tan x)}$ ${\\ y\prime\prime=\tan x +\cos x ln(\sec x +\tan x)}$

Substituindo a derivada de segunda ordem na ED teremos:

$\displaystyle y\prime\prime+y=[\tan x +\cos x \ln(\sec x +\tan x)]+[-(\cos x)\ln(\sec x+ tan x)]=\tan x$

Exercício 2.Comprove que a expressão indicada é uma solução implícita da equação diferencial dada

${\dfrac{dx}{dt}=(x-1)(1-2x);}$ ${ \ln (\dfrac{2x-1}{x-1})=t }$

Encontre pelo menos uma solução explicita

Solução:escrevendo ${\ln(2x-1)-\ln(x-1)=t}$ e derivando, teremos: ${\dfrac{2}{2x-1}\dfrac{dx}{dt}-\dfrac{1}{x-1}\dfrac{dx}{dt}=1}$ ${\Rightarrow}$ ${(\dfrac{2}{2x-1}-\dfrac{1}{x-1})\dfrac{dx}{dt}=1}$

${\dfrac{2x-2-2x+1}{(2x-1)(x-1)}\dfrac{dx}{dt}=1}$ ${\Rightarrow }$ ${\dfrac{dx}{dt}=-(2x-1)(x-1)\Rightarrow}$ ${\dfrac{dx}{dt}=(x-1)(1-2x)}$

Para acharmos a solução explicita temos que isolar x na solução implícita fazendo:

${(\dfrac{2x-1}{x-1})=e^{t}\Rightarrow}$ ${ 2x-1=xe^{t}-e^{t}\Rightarrow }$ ${(e^{t}-1)=(e^{t}-2)x }$ A solução explicita será: ${ x=\dfrac{(e^{t}-1)}{(e^{t}-2)} }$

Exercício 3.Verifique se a família de funções dada é uma solução da equação diferencial.

${ \dfrac{dy}{dx}+2xy=1;}$ ${y=e^{-x^{2}}\int_0^x e^{t^{2}}dt+c_{1}e^{-x^{2}}}$
Solução:Derivando a função ${ y=e^{-x^{2}}\int_0^x e^{t^{2}}dt+c_{1}e^{-x^{2}} }$ obtemos: ${ y\prime=e^{-x^{2}}e^{x^{2}}-2xe^{-x^{2}}\int_0^x e^{t^{2}}dt-2c_{1}xe^{-x^{2}}\Rightarrow}$ ${y\prime=1-2xe^{-x^{2}}\int_0^x e^{t^{2}}dt-2c_{1}xe^{-x^{2}}}$ substituindo a derivada na equação diferencial teremos: ${\dfrac{dy}{dx}+2xy=1-2xe^{-x^{2}}\int_0^x e^{t^{2}}dt-2c_{1}xe^{-x^{2}}+2xe^{-x^{2}}\int_0^x e^{t^{2}}dt+2xc_{1}e^{-x^{2}}}$

$\displaystyle \dfrac{dy}{dx}+2xy=1$
${\dfrac{d^{2}y}{dx^{2}}-4\dfrac{dy}{dx}+4y=0; }$ ${ y=c_{1}e^{2x}+c_{2}xe^{2x}}$
Solução:Derivando a função ${ y=c_{1}e^{2x}+c_{2}xe^{2x} }$ teremos: ${\dfrac{dy}{dx}=(2c_{1}+c_{2})e^{2x}+2c_{2}xe^{2x}}$ ${\\ \dfrac{d^{2}y}{dx^{2}}=(4c_{1}+4c_{2})e^{2x}+4c_{2}xe^{2x}}$

substituindo as derivadas na equação diferencial teremos: ${\dfrac{d^{2}y}{dx^{2}}-4\dfrac{dy}{dx}+4y=(4c_{1}+4c_{2})e^{2x}+4c_{2}xe^{2x}-4[(2c_{1}+c_{2})e^{2x}+2c_{2}xe^{2x}]+c_{1}e^{2x}+c_{2}xe^{2x}}$

${\\ \dfrac{d^{2}y}{dx^{2}}-4\dfrac{dy}{dx}+4y=(4c_{1}+4c_{2}-8c_{1}-4c_{2})e^{2x}-(4c_{2}-8c_{2}+4c_{2})xe^{2x}=0}$

Exercício 4:A função ${y=1/(1+c_{1}e^{-x}) }$ é uma família de soluções da ED de primeira ordem ${ y\prime=y-y^{2}.}$ Determine uma solução para o problema de valor inicial que consiste nesta ED e na condição inicial ${ y(0)=-\frac{1}{3}.}$

Solução:substituindo as condições iniciais na função, teremos:

$\displaystyle -\dfrac{1}{3}=\dfrac{1}{1+c_{1}}$

Determinando valor de ${c_{1}}$ teremos: ${c_{1}=-4}$

Substituindo o valor de ${c_{1}}$ na função teremos: ${y=1/(1-4e^{-x})}$

Exercício 5:A função ${y=c_{1}e^{x}+c_{2}e^{-x}}$ é uma família de soluções da ED de segunda ordem ${ y\prime\prime-y=0.}$ Determine uma solução para o problema de valor inicial que consiste nesta ED e nas seguintes condições iniciais: ${y(0)=1,}$ ${y\prime(0)=2}$

Solução:determinando a primeira derivada da função temos:

$\displaystyle y\prime=c_{1}e^{x}-c_{2}e^{-x}$

substituindo as condições iniciais ${y(0)=1,}$ ${y\prime(0)=2}$ na função e na primeira derivada temos:

$\displaystyle \begin{cases} c_{1}+c_{2}=1\\ c_{1}-c_{2}=2 \end{cases}$

Determinando valor de ${c_{1}}$ e ${c_{2}}$ teremos: ${c_{1}=\dfrac{3}{2}}$ e ${c_{2}=-\dfrac{1}{2}}$

Substituindo o valor de ${c_{1}}$ e ${c_{2}}$ na função teremos: ${y=\dfrac{3}{2}e^{x}-\dfrac{1}{2}e^{-x}}$

Exercício 6.Determine uma região do plano xy para a qual a equação diferencial ${ (1+y^{3})y\prime=x^{2} }$ teria uma única solução passando por um ponto ${(x_{0},y_{0})}$ na região.

Solução:Pelo Teorema de Picard temos: ${ f(x,y)=\dfrac{x^{2} }{(1+y^{3})} }$

Derivando a função temos: ${ \dfrac{\partial f}{\partial y}=\dfrac{-3x^{2}y^{2}}{(1+y^{3})^{2}}}$ assim, a equação diferencial terá uma única solução, em qualquer região, onde ${ y\neq-1 }$

Exercício 7.Verifique se o Teorema de Picard garante unicidade de solução para a equação diferencial ${ y\prime=\sqrt{y^{2}-9},}$ passando pelo ponto dado:

(1,4)
(5,3)

Solução:Pelo Teorema de Picard temos que: ${ f(x,y)=\sqrt{y^{2}-9} }$

Derivando a função temos: ${ \dfrac{\partial f}{\partial y}=\dfrac{y}{\sqrt{y^{2}-9}} }$ assim, a equação diferencial terá uma única solução, em qualquer região, onde ${y>3.}$ então:

a equação diferencial tem uma única solução no ponto (1,4).
a equação diferencial não garante uma única solução no ponto (5,3).

Luso Academia

Category Archives: 19 Cálculo IV

Equações diferenciais homogéneas.Exercícios resolvidos

Equações diferenciais de variáveis separáveis.Exercícios resolvidos

Aplicação das equações diferenciais de primeira ordem.Misturas

Aplicação das equações diferenciais de primeira ordem.Corpos em queda

Aplicação das equações diferenciais de primeira ordem.Circuitos elétricos

Aplicações das equações diferenciais de primeira ordem.

Equações diferenciais de Bernoulli e Ricatti. Redução a separação de variáveis

Equações Diferenciais Exatas e Lineares

2. Equações Diferenciais de Primeira ordem

1. Exercícios Resolvidos de Equações Diferenciais

Navegação de artigos

Category Archives: 19 Cálculo IV

Partilhar

Partilhar

Partilhar

Partilhar

Partilhar

Partilhar

Partilhar

Partilhar

Partilhar

Partilhar

Navegação de artigos