07/25/2015 6:53 pm / 1 comentário em Mecânica Quântica – Revisões VI
— 19. Resolução de Exercícios —
| Exercício 3 Derive as transformações de equações para um pêndulo duplo.
Temos:
|
| Exercício 4 Mostre que é:

Temos
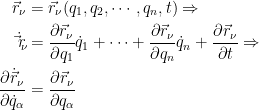
Que é o resultado pretendido
|
Exercício 5 Considere um conjunto de partículas que descrevem um incremento  nas suas coordenadas generalizadas. Derive a seguinte expressão nas suas coordenadas generalizadas. Derive a seguinte expressão  para o trabalho total realizado pela força que actua no sistema e interprete fisicamente o factor para o trabalho total realizado pela força que actua no sistema e interprete fisicamente o factor 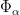 . .
Primeiro vamos notar que é
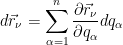
Para  é é
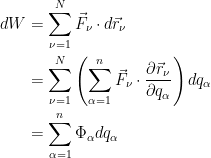
e 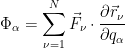 é a força generalizada. é a força generalizada.
|
Exercício 6 Mostre que  . .
Temos
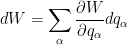
e
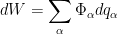
Logo
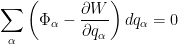
Uma vez que  são linearmente independentes (ou se preferir, são arbitrários) vem que são linearmente independentes (ou se preferir, são arbitrários) vem que  . .
|
| Exercício 7 Derive o lagrangiano de um pêndulo simples e obtenha as equações de movimento
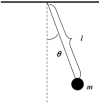
A coordenada generalizada para o pêndulo simples é  e as equações de transformação de coordenadas são e as equações de transformação de coordenadas são  and and  . .
A energia cinética é 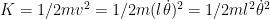 . .
A energia potencial é  . .
Assim o lagrangiano é
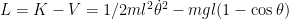
Uma vez que temos
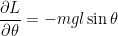
e
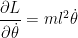
E a equação de Euler-Lagrange fica
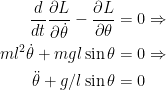
|
| Exercício 8
Duas partículas de massa  estão ligadas entre si e a duas paredes por molas de constante estão ligadas entre si e a duas paredes por molas de constante 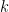 . As partículas deslocam-se ao longo de uma direcção. Use as equações de Euler-Lagrange para descrever o movimento das massas. . As partículas deslocam-se ao longo de uma direcção. Use as equações de Euler-Lagrange para descrever o movimento das massas.

A energia cinética é 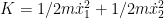 . .
A energia potencial é 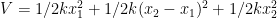 . .
Logo o lagrangiano é 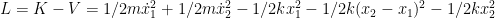 . .
As derivadas parciais do lagrangiano são:
E as equações de Euler-Lagrange ficam:
|
| Exercício 9
Uma partícula de massa  move-se sob a acção de um campo central e conservativo. Use coordenadas cilíndricas para derivar: move-se sob a acção de um campo central e conservativo. Use coordenadas cilíndricas para derivar:
- O lagrangiano A energia cinética é
 . A energia potencial é . A energia potencial é  . Logo o lagrangiano é . Logo o lagrangiano é
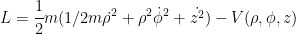
- As equações de movimento
|
Exercício 10 Para um duplo pêndulo calcule:
- O lagrangiano
As equações para as transformações de coordenadas são
Aplicando 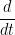 às equações anteriores às equações anteriores
Logo a energia cinética é
![\displaystyle K=1/2m_1l^2_1\theta^2_1+1/2m\left[ l^2_1\dot{\theta}^2_1+l^2_2\dot{\theta}^2_2+2l_1l_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2) \right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++K%3D1%2F2m_1l%5E2_1%5Ctheta%5E2_1%2B1%2F2m%5Cleft%5B+l%5E2_1%5Cdot%7B%5Ctheta%7D%5E2_1%2Bl%5E2_2%5Cdot%7B%5Ctheta%7D%5E2_2%2B2l_1l_2%5Cdot%7B%5Ctheta%7D_1%5Cdot%7B%5Ctheta%7D_2%5Ccos%28%5Ctheta_1-%5Ctheta_2%29+%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
E a energia potencial é
![\displaystyle V=m_1g(l_1+l_2-l_1\cos\theta_1)+m_2g\left[l_1+l_2-(l_1\cos\theta_1+l_2\cos\theta_2)\right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+V%3Dm_1g%28l_1%2Bl_2-l_1%5Ccos%5Ctheta_1%29%2Bm_2g%5Cleft%5Bl_1%2Bl_2-%28l_1%5Ccos%5Ctheta_1%2Bl_2%5Ccos%5Ctheta_2%29%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
Como sempre o lagrangiano é 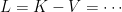
- As equações de movimento
Assim é
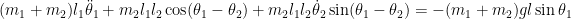
e

- Faça
 e e  e escreva as equações de movimento. e escreva as equações de movimento.
Fica como um exercício para o leitor.
- Escreva as equações anteriores no limite das pequenas oscilações.
Se 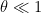 sabemos que sabemos que 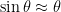 e e 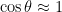 . .
E as equações de movimento ficam
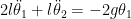
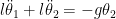
|
Exercício 11 Uma partícula move-se no plano 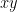 sujeita a uma força central que é uma função da distância entre a partícula e a origem. sujeita a uma força central que é uma função da distância entre a partícula e a origem.
- Calcule o Hamiltoniano do sistema.
As coordenadas generalizadas são  e e  . .
A energia potencial é da forma  . .
O lagrangiano é  . .
Os momentos conjugados são:
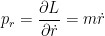
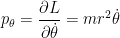
O Hamiltoniano fica
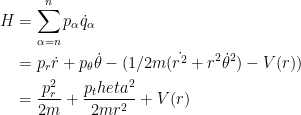
- Escreva as equações de movimento:
|
| Exercício 12
Uma partícula descreve um movimento unidimensional sujeita a uma força da forma
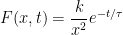
Onde 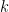 e e  são constantes positivas. Calcule o lagrangiano e hamiltoniano. Compare o hamiltoniano com a energia total e discuta se existe conservação de energia para este sistema. são constantes positivas. Calcule o lagrangiano e hamiltoniano. Compare o hamiltoniano com a energia total e discuta se existe conservação de energia para este sistema.
Uma vez que  vem que vem que 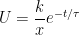 . .
Para a energia cinética é 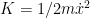 . Assim o lagrangiano é . Assim o lagrangiano é

Ora  . .
E o hamiltoniano é

Uma vez que 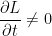 o sistema não é conservativo. o sistema não é conservativo.
Uma vez que 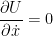 sabemos que é sabemos que é  . .
|
| Exercício 13
Considere duas funções das coordenadas generalizadas e os momentos generalizados,  e e  . O parênteses de Poisson é definido como: . O parênteses de Poisson é definido como:
![\displaystyle [g,h]=\sum_k \left(\frac{\partial g}{\partial q_k}\frac{\partial h}{\partial p_k}-\frac{\partial g}{\partial p_k}\frac{\partial h}{\partial q_k}\right)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Bg%2Ch%5D%3D%5Csum_k+%5Cleft%28%5Cfrac%7B%5Cpartial+g%7D%7B%5Cpartial+q_k%7D%5Cfrac%7B%5Cpartial+h%7D%7B%5Cpartial+p_k%7D-%5Cfrac%7B%5Cpartial+g%7D%7B%5Cpartial+p_k%7D%5Cfrac%7B%5Cpartial+h%7D%7B%5Cpartial+q_k%7D%5Cright%29+&bg=ffffff&fg=000000&s=0&c=20201002)
Mostre que as seguintes propriedades do parênteses de Poisson são válidas:
-
![{ {\dfrac{dg}{dt}=[g,H]+\dfrac{\partial g}{\partial t}}}](https://s0.wp.com/latex.php?latex=%7B+%7B%5Cdfrac%7Bdg%7D%7Bdt%7D%3D%5Bg%2CH%5D%2B%5Cdfrac%7B%5Cpartial+g%7D%7B%5Cpartial+t%7D%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . .
Fica como um exercício para o leitor.
-
![{ {\dot{q}_j=[q_j,H]}}](https://s0.wp.com/latex.php?latex=%7B+%7B%5Cdot%7Bq%7D_j%3D%5Bq_j%2CH%5D%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) e e ![{ {\dot{p}_j=[p_j,H]}}](https://s0.wp.com/latex.php?latex=%7B+%7B%5Cdot%7Bp%7D_j%3D%5Bp_j%2CH%5D%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . .
Fica como um exercício para o leitor.
-
![{ {[p_k,p_j]=0}}](https://s0.wp.com/latex.php?latex=%7B+%7B%5Bp_k%2Cp_j%5D%3D0%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) e e ![{ {[q_k,q_j]=0}}](https://s0.wp.com/latex.php?latex=%7B+%7B%5Bq_k%2Cq_j%5D%3D0%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . .
Fica como um exercício para o leitor.
-
![{ {[q_k,p_j]=\delta_{ij}}}](https://s0.wp.com/latex.php?latex=%7B+%7B%5Bq_k%2Cp_j%5D%3D%5Cdelta_%7Bij%7D%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . .
Fica como um exercício para o leitor.
- Mostre que se uma função
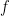 não depende explicitamente de não depende explicitamente de  então então ![{ {[f,H]=0}}](https://s0.wp.com/latex.php?latex=%7B+%7B%5Bf%2CH%5D%3D0%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . . 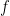 diz-se uma constante de movimento. diz-se uma constante de movimento.
Fica como um exercício para o leitor.
Se o parênteses de Poisson entre duas funções é nulo então dizemos que as duas funções comutam. |



