Luso Academia

Início » 04 Ensino Superior » 02 Física » Equações diferenciais de Bernoulli e Ricatti. Redução a separação de variáveis

Equações diferenciais de Bernoulli e Ricatti. Redução a separação de variáveis

Estatística do blog

  • 1.021.782 académicos

De modo a receber actualizações do nosso blog via email clique em Seguir.

Junte-se a 5.486 outros subscritores

— 2.5. Equação de Bernoulli —

Neste artigo, não estudaremos nenhum tipo particular para equação diferencial.Consideraremos duas equações clássicas que podem ser transformadas em equações já estudadas nas seções anteriores e depois vamos abordar sobre redução a separação de variáveis.

Definição 14.A equação diferencial

\displaystyle \dfrac{dy}{dx}+P(x)y=Q(x)y^{n} \ \ \ \ \ (11)

em que n é um numero real qualquer, é chamada de equação de Bernoulli.Para {n=0} e {n=1} a equação (11) é linear em y.Agora se {y\neq0},a equação (11) pode ser escrita da seguinte maneira:

\displaystyle y^{-n}\dfrac{dy}{dx}+P(x)y^{1-n}=Q(x) \ \ \ \ \ (12)

se fizermos {w=y^{1-n},\quad n\neq0,\quad n\neq1,} então:

\displaystyle \dfrac{dw}{dx}=(1-n)y^{-n}\dfrac{dy}{dx}

com essa substituição, a equação (12) transforma-se na equação linear

\displaystyle \dfrac{dw}{dx}+(1-n)P(x)w=(1-n)Q(x) \ \ \ \ \ (13)

Resolvendo a equação (13) e depois fazendo {y^{1-n}=w}, obtemos uma solução para a equação (11).

Exemplo 1.Resolva a seguinte equação

\displaystyle \dfrac{dy}{dx}+\dfrac{1}{x}y=xy^{2}

Solução:De acordo a equação de Bernoulli temos:{P(x)=1/x,\quad Q(x)=x, \quad e \quad n=2}.logo, a mudança de variável

\displaystyle w=y^{-1}\Rightarrow \dfrac{dw}{dx}=-y^{-2}\dfrac{dy}{dx}\Rightarrow \dfrac{dy}{dx}=-y^{2}\dfrac{dw}{dx}

nos da o seguinte:

\displaystyle -y^{2}\dfrac{dw}{dx}+\dfrac{1}{x}y=xy^{2}\Rightarrow \dfrac{dw}{dx}-\dfrac{1}{x}y^{-1}=-x

substituindo {w=y^{-1}} teremos:

\displaystyle \dfrac{dw}{dx}-\dfrac{1}{x}w=-x

o fator de integração para essa equação linear é:

\displaystyle \mu(x)=e^{-\int \frac{dx}{x}}=e^{-ln x}=x^{-1}

assim,multiplicando o fator de integração na equação linear, teremos:

\displaystyle x^{-1}\dfrac{dw}{dx}-x^{-2}w=-1\Rightarrow \dfrac{d}{dx}(x^{-1}w)=-1

integrando essa ultima forma, obtemos

\displaystyle x^{-1}w=-x+c \quad ou \quad w=-x^{2}+cx

como {w=y^{-1}}, então {y=\frac{1}{w}} ou

\displaystyle y=\dfrac{1}{-x^{2}+cx}

— 2.6. Equação de Ricatti —

Definição 15.A equação diferencial linear

\displaystyle \dfrac{dy}{dx}=P(x)+Q(x)y+R(x)y^{2} \ \ \ \ \ (14)

é chamada de equação de Ricatti.Se {y_{1}} é uma solução particular para (14),então as substituições

\displaystyle y=y_{1}+u \quad e \quad \dfrac{dy}{dx}=\dfrac{dy_{1}}{dx}+\dfrac{du}{dx}

em (14) produzem a seguinte equação diferencial para u:

\displaystyle \dfrac{du}{dx}-(Q+2y_{1}R)u=Ru^{2} \ \ \ \ \ (15)

como (15) é uma equação de Bernoulli com {n=2}, ela pode, por sua vez, ser reduzida a equação linear

\displaystyle \dfrac{du}{dx}+(Q+2y_{1}R)u=-R \ \ \ \ \ (16)

através da substituição {w=u^{-1}}.Depois de fazer essa substituição podemos aplicar os outros métodos estudados.

Exemplo 2.Considere a equação

\displaystyle \dfrac{dy}{dx}=e^{2x}+(1+2e^{x})y+y^{2}

Verifica-se que {y_{1}=-e^{x}} é uma solução particular desta equação.Fazendo a substituição

\displaystyle y=-e^{x}+u\Rightarrow \dfrac{dy}{dx}=-e^{x}+\dfrac{du}{dx}

teremos:

\displaystyle -e^{x}+\dfrac{du}{dx}=e^{2x}+(1+2e^{x})(-e^{x}+u)+(-e^{x}+u)^{2}

simplificando a equação obtemos a seguinte expressão

\displaystyle \dfrac{du}{dx}=u+u^{2}

a equação acima é uma equação de Bernouli, então,vamos fazer a seguinte substituição:

\displaystyle w=u^{-1}\Rightarrow \dfrac{dw}{dx}=-y^{-2}\dfrac{du}{dx}\Rightarrow \dfrac{du}{dx}=-u^{2}\dfrac{dw}{dx}

logo, teremos:

\displaystyle -u^{2}\dfrac{dw}{dx}=u+u^{2}\Rightarrow \dfrac{dw}{dx}=-\dfrac{1}{u}-1\Rightarrow \dfrac{dw}{dx}=-w-1

a ultima equação é de variáveis separáveis de modo que resolvendo teremos:

\displaystyle ln (w+1)=-x+c_{1}\Rightarrow w=e^{-x+c_{1}}-1\Rightarrow w=ce^{-x}-1

substituindo {w=u^{-1}} temos:

\displaystyle u^{-1}=ce^{-x}-1\Rightarrow u=\dfrac{1}{ce^{-x}-1}

substituindo {u=y+e^{x}} obtemos que a solução da equação é dada por:

\displaystyle y=\dfrac{1}{ce^{-x}-1}-e^{x}

— 2.7. Redução a Separação De Variáveis —

Definição 16.Uma equação diferencial da forma

\displaystyle \dfrac{dy}{dx}=f(Ax+By+c)

se pode sempre reduzir a uma equação com variáveis separáveis por meio da substituição {u=Ax+By+c}, {B\neq0}

Exemplo 3.Resolva a seguinte equação diferencial

\displaystyle \dfrac{dy}{dx}=(-2x+y)^{2}-7, \quad y(0)=0

Solução:Vamos resolve-la fazendo a substituição

\displaystyle u=-2x+y\Rightarrow \dfrac{du}{dx}=-2+\dfrac{dy}{dx}

dessa maneira a equação diferencial se expressa da seguinte forma:

\displaystyle \dfrac{du}{dx}+2=u^{2}-7\Rightarrow \dfrac{du}{dx}=u^{2}-9

essa ultima equação é de variáveis separáveis de modo que teremos:

\displaystyle \dfrac{du}{(u-3)(u+3)}=dx\Rightarrow \dfrac{1}{6}\left[\dfrac{1}{u-3}-\dfrac{1}{u+3}\right]du=dx

e depois de integrar vamos ter:

\displaystyle \dfrac{1}{6}ln \left[\dfrac{u-3}{u+3}\right]=x+c_{1}\Rightarrow \dfrac{u-3}{u+3}=e^{6x+6c_{1}}

substituindo {e^{6c_{1}}} por c e isolando u obtemos o seguinte:

\displaystyle u=\dfrac{3(1+ce^{6x})}{1-ce^{6x}}

substituindo {u=-2x+y} na equação acima obtemos a seguinte solução:

\displaystyle y=2x+\dfrac{3(1+ce^{6x})}{1-ce^{6x}}

por ultimo aplicando a condição inicial {y(0)=0} a ultima equação obtém-se {c=-1} de modo que a solução particular será:

\displaystyle y=2x+\dfrac{3(1-e^{6x})}{1+e^{6x}}

a figura abaixo mostra em azul escuro o gráfico da solução particular junto com o gráfico de outros membros da família de soluções.

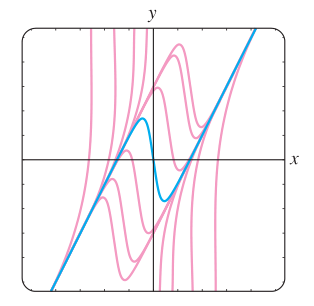
eqdf3

Figura 1:Algumas soluções do Exemplo 3

Nas seções precedentes, vimos que em certas situações uma equação diferencial podia ser ser transformada, por meio de uma substituição, em uma forma em que era possível resolve-la por um método padrão.Uma equação pode parecer diferente de todas as que vimos e estudamos, mas mudando uma variável, talvez um problema aparentemente difícil possa ser facilmente resolvido.Embora não haja uma regra geral que indique qual substituição deve ser feita,uma axioma pratico é o seguinte:tente alguma coisa!Algumas vezes custa caro ser engenhoso.

Exemplo 4.Considere a equação

\displaystyle \dfrac{dy}{dx}=\dfrac{y-x}{y-x-1}

se olharmos bem a equação, podemos ser impelidos a tentar a substituição

\displaystyle u=y-x\Rightarrow \dfrac{du}{dx}=\dfrac{dy}{dx}-1\Rightarrow \dfrac{dy}{dx}=\dfrac{du}{dx}+1

substituindo na equação temos:

\displaystyle \dfrac{du}{dx}+1=\dfrac{u}{u-1}\Rightarrow \dfrac{du}{dx}=\dfrac{1}{u-1}\Rightarrow (u-1)\dfrac{du}{dx}=1

que é uma equação de variável separável cuja solução é:

\displaystyle \dfrac{u^{2}}{2}-u=x+c

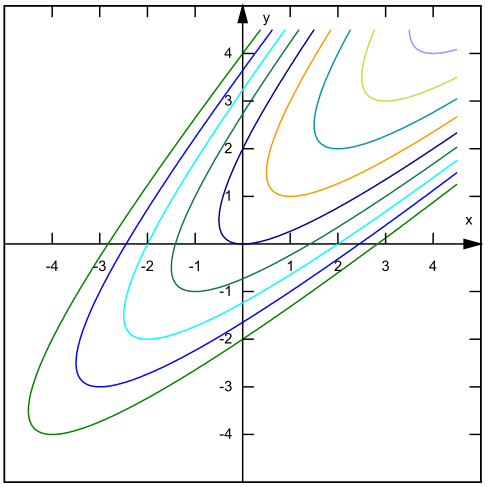
Substituindo-se de volta {u=y-x} obtemos que a solução da equação é dada implicitamente por

\displaystyle \dfrac{(y-x)^{2}}{2}-y=c

eqdf4

Figura 2:soluções da equação do Exemplo 4

By in 02 Física, 04 Ensino Superior, 19 Cálculo IV on .

3 comentários

  1. Belmiro diz:
    05/17/2016 às 10:36 am

    Bom dia Prof. Maitsuda tenho uma pequena dúvida:
    Na equaçao de Bernoulli quando fazemos W=y^1-n. O “n” deve ser o maior grau da nossa equaçao ou deverá ser o grau da variável que multiplica “Q(x)”?

    Se for o grau da variável que multiplica Q(x), nos casos em que temos na equação Q(x)/y^2 por exemplo, podemos considerar “n”= -2??

    Liked by 1 person

    Responder
  2. Belmiro diz:
    05/17/2016 às 10:37 am

    Bom dia Prof. Maitsuda tenho uma pequena dúvida:
    Na equaçao de Bernoulli quando fazemos W=y^1-n. O “n” deve ser o maior grau da nossa equaçao ou deverá ser o grau da variável que multiplica “Q(x)”?

    Se for o grau da variável que multiplica Q(x), nos casos em que temos na equação Q(x)/y^2 por exemplo, podemos considerar “n”= -2?

    Liked by 1 person

    Responder
  3. Bruna Brasil diz:
    10/23/2016 às 11:04 pm

    boa tarde, na equação y’ + (1-2x)y = xe^-x. Q(x) = -x?

    Gostar

    Responder

Deixe um comentário

Este site utiliza o Akismet para reduzir spam. Fica a saber como são processados os dados dos comentários.

Donativos

Donate Button

Localização

wordpress com stats